Complément de mathématique
Les nombres complexes
Insuffisance de IR
Dans R on ne peut pas trouver la racine carrée d'un nombre négatif, il existe donc un ensemble plus grand que R appelé ensemble des nombres complexes noté C qui permet d'extraire des racines des nombres négatifs. j est appelé opérateur complexe.
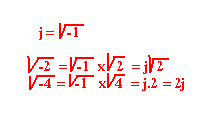
La propriété importante des nombres complexes:
- j2 = -1
- j3 = j2 x j = -j
- j4 = j2 x j2 = -1(-1) = 1
Définition des nombres complexes
Il existe 5 façons de représenter un nombre complexe mais on étudiera que 3 dans ce cours.
La forme algébrique
Quelque soit z appartenant à C; z=a+jb (a, b) appartient à R2.
- a: partie réelle
- b: partie imaginaire
La forme trigonométrique
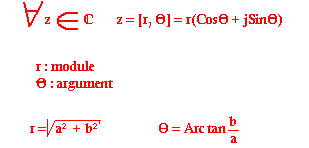
La forme polaire
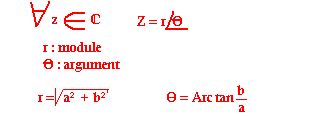
Quelques propriétés
Soient z et z' deux nombres complexes z=a+jb et z'=a'+jb'
- z = 0 si et seulement si a = b = 0
- z + z' = a + jb + a' + jb'
=a + a' + j(b + b')
= A + jB avec A = a+ a' et B = b + b' - z - z' = a + jb - (a' + jb')
= a - a' + j(b - b')
= A + jB avec A = a - a' et B = b - b' - z.z' = (a + jb)(a' + jb')
= aa' + jab' + ja'b + j2bb'
= aa' - bb' + j(ab' + a'b)
= A + jB avec A = aa' - bb' et B = ab' + a'b 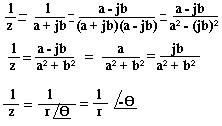
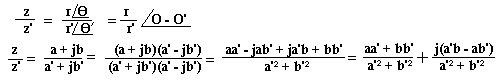
- z = z' ↔ a = a' et b = b'
Conjugué d'un nombre complexe
On appelle conjugué d'un nombre complexe de coordonnée a+jb le nombre complexe z' tel que:
![]()
Exemple
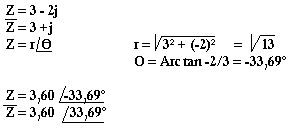
Propriétés
Soient Z = a +jb et Z' = a' + jb'
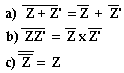
Quelques formules trigonométriques
Propriétés
- Cos(-x) = Cosx
Sin(-x) = Sinx - Cos2x + Sin2x = 1
- tgx = Sinx/Cosx cotgx = Cosx/Sinx
Formules de transformations
- Cos(a+b) = CosaCosb - SinaSinb
- Cos(a-b) = CosaCosb + SinaSinb
- Sin(a+b) = SinaCosb + SinbCosa
- Sin(a-b) = SinaCosb - SinbCosa
- tg(a+b) = (tga+tgb)/(1-tga.tgb)
- tg(a-b) = (tga-tgb)/(1+tga.tgb)
- Cosp + Cosq = 2Cos(p/2+q/2)Cos(p/2-q/2)
- Cosp - Cosq = -2sin(p/2 + q/2)Sin(p/2 - q/2)
- Sin + Sinq = 2Sin(p/2 + q/2)Cos(p/2-q/2)
- Sinp - sinq = 2sin(p/2-q/2)Cos(p/2+q/2)