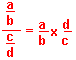Soit A un sous ensemble non vide de R.

Exemple:

Z = {..., -1, 0, 1, 2...}
Z, Q, R ne sont ni minorés ni majorés.
N = {0, 1, 2, 3...}

L'ensemble R n'est pas majoré mais 0, -1, -2, -II, etc. sont des minorants de N.

Un sous ensemble majoré (respectivement minoré) de R admet une infinité de majorant (respectivement minorant). En effet si M est majorant (respectivement minorant) tous nombre supérieur à M (respectivement < M) est aussi un majorant (respectivement minorant).

Soit A un sous ensemble non vide de R.

Exemple:

N = {0, 1, 2, 3...}
Minorant: 0; 1-; -2; -II; etc.
Le plus petit élément de N est 0.
Le plus minimum de N est 0.
Toute partie finie de R admet un maximum et un minimum.
Exemple: Le segment [0; 5] a pour minimum 0 et de  maximum 5.

Calcul approché

Encadrement des réels

Encadrement d'un réel par des nombres décimaux

Soit x=7/3; 2,33 ← 7/3 ← 2,34 à 10^-2 ou 1/100 près. 2,33 est la valeur approchée de x=7/3 à 10^-2 par défaut. 2,34 est la valeur approchée de x=7/3 à 10^-2 par excès.

Incertitude

Soit x et y deux nombres réels E>0 un réel strictement positif. y est une valeur approchée de x à E près signifie que |x-y|←E. Le nombre réel E est appelé incertitude de cette valeur approchée.
|x-y| est appelée distance de x à y.

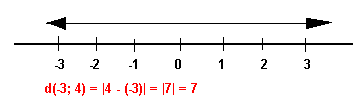
Valeur approchée d'une somme

Si x₀ est une valeur approchée d'un réel x avec pour incertitude Þ et y₀ une valeur approchée d'un réel y avec pour incertitude ß. x₀+y₀ est la valeur approchée de x+y avec une incertitude égale à Þ+ß.
Exemple: Soient les encadrements

Calcul de la valeur approchée:
x₀ = (8,032+8,046)/2 = 8,039 et Þ= (8,046-8,032)/2
Þ=0,007
y₀ = (5,24+5,50)/2 = 5,37 et ß= (5,24+5,50)/2
ß=0,13
La somme x₀+y₀ a pour incertitude Þ+ß=0,13+0,004=0,137

Fractions

Somme

a, b, c, d sont des nombres, b et d ne sont pas nuls.

Multiplication

Quotient