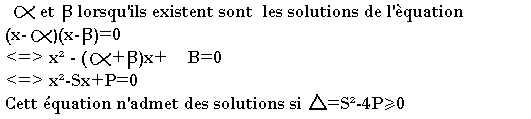Equations du second degré
Polynôme du second degré
Un polynôme du second degré est toute application f:R→R qui à toute valeur de x associe f(x)=ax2+bx+c avec a appartenant à R*, b appartenant à R; c appartenant à R.
Mise sous forme canonique d'un polynôme du second degré
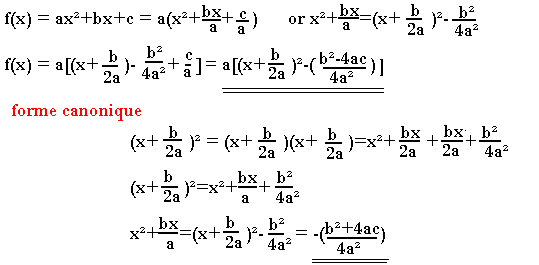
Equation du second degré
On appelle équation du second degré, toute expression de la forme ax2+bx+c=0 avec a appartenant à IR*; b appartenant à R; c appartenant à R
Résolution
La résolution de ce type d'équation est dépendante du discriminant D=b2-4ac
- Si D<0 , l'équation n'admet aucune racine réelle S=Ø
- Si D>0 , l'équation admet deux racine distincte:
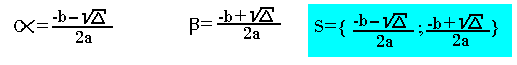
- Si D=0, l'équation admet une racine
Exercice: Résolution d'une équation bicarrée.
x4 - 4x2 - 45 = 0
↔ (x2)2 - 4x2 - 45 = 0
Posons X = x2
X2 - 4X - 45 = 0
D = (-4)2 - 4(-45) = 196 = 142
X1 = ½(4-14) = -5 ; X2 = ½(4+14) = 9
Comme x2 = X
↔ x2 = -5 (impossible)
↔ x2 = 9 équivaut à x = 3 ; x = -3
S = {-3 ; 3}
Signe du polynôme du second degré
Soit le polynôme f(x)=ax2+bx+c avec a différent de 0
- Si Δ<0 ax2+bx+c est du signe de a pour tout signe réel
- Si Δ=0 le polynôme ax2+bx+c est du signe de a
- Si Δ>0 le polynôme ax2+bx+c possède 2 racines réelles distincte
Théorème:
Le polynôme du second degré ax2+bx+c avec Δ>0 est du signe de a à l'extérieur des racines et du signe contraire de a à l'intérieur.
Somme et produit des racines
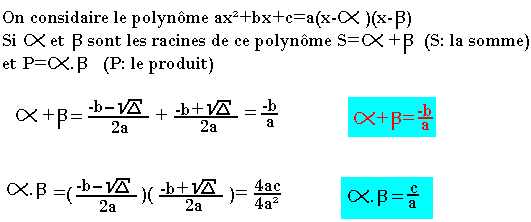
Recherche de deux nombres connaissant leur somme et leur produit
Concours d'entrée aux grandes écoles
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale