Intégrales doubles
Intégrale double sur un rectangle
ƒ est continue sur [a, b]*[c, d] a<b, c<d.
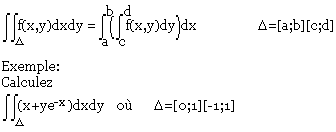
Intégrale double sur un ouvert borné
D = ouvert borné non vide R2
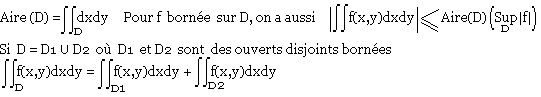
Intégrations successives
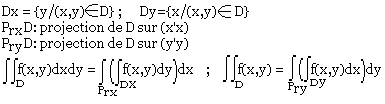
Cas de "variables séparées".
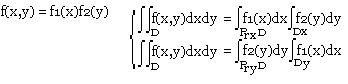
Exemples de calcul:
ƒ(x, y) = xy2 ; D: domaine limité par les droites x=2 ; x=-2 ; l'hyperbole y2-x2=1
Valeur moyenne d'une fonction sur le domaine borné D
f est une fonction sur D. La valeur moyenne de f sur D est :
Exemple:
Calculez la valeur moyenne de ƒ(x ,y)=xy2 sur:
Changement de variables
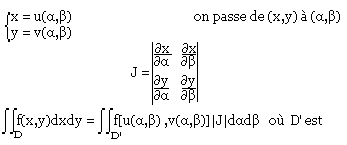
Le domaine image de D par la transformation
Exemple:
(S) = cercle de centre O(0; 0) et rayon 2.
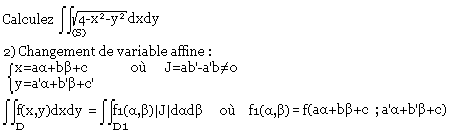
et D1 est image de D dans le plan de variable cartésienne.
Exemple:
Calculez.
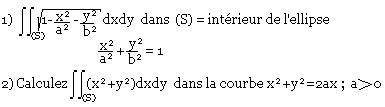
Calcul d'aires
- En coordonnées rectangulaires (cartésienne)
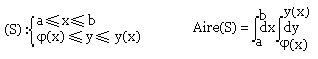
- En coordonnées polaire: (r, φ)
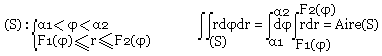
Exemple:
(S) est le domaine limité par x2=2y ; x2=4y (posez x2=4y ; y2=vx)
Calcul de volume
On considère dans l'espace (o, i, j, k) un cylindre limité supérieurement par une surface continue et inférieurement par z=0
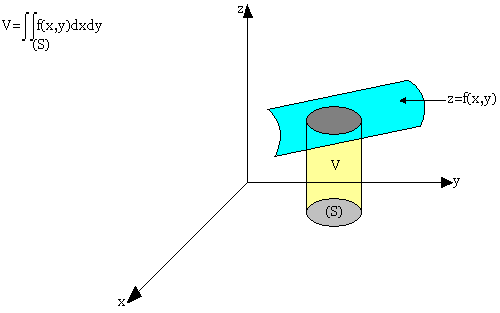
Exercice:
Calculez le volume limité par;
- Le paraboloïde elliptique z=2x2+y2+1, le plan x+y=1 et les plans de coordonnées.
- Le paraboloïde hyperbolique z=x2-y2 et les plans y=0, z=0 et x=1
- Les surfaces: 2z+x2+y2 ; x2+y2=1 ; z=0
Calculez le volume de l'ellipsoïde:
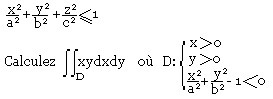
Calcul d'axe de surfaces de R3
Une surface de R3 est donnée par z=ƒ(x, y, z) ou F(x, y, z)=0 ou une caractérisation paramétrique.
Exemple:
- (S): surface du cône x2-y2=z2 comprise dans le premier dièdre et limité par le plan y+z=a ; a>0
- Calculez l'aire de la portion de surface d'une parabole de y2+z2=2ax comprise entre le cylindre y2=ax et le plan x=a ; a>0
Application de l'intégrale double
Masse et segment statique d'une plaque.
(S) : domaine du plan (xoy) : plaque
φ(x, y) : densité superficielle
M : masse de cette plaque
Mx et My sont les moments statiques de la plaque par rapport aux axes (ox) et (oy).
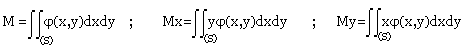
Les coordonnées du centre de masse G sont x=My/M ; y=Mx/M
Moment d'inertie par rapport aux axes (ox), (oy)
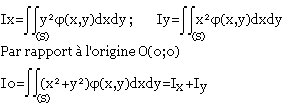
Exercices:
- (S) : plaque limitée par y=Sinx ; OA où A(3,14/2;1) de densité φ(x,y)=xy.
Trouvez les coordonnées du centre de masse. - Calculez le moment d'inertie du carré de côté a par rapport à l'axe qui passe par sa son sommet et qui est perpendiculaire au plan du carré.
Concours d'entrée aux grandes écoles
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale