Un solide est en mouvement de rotation lorsque ses différents points décrivent des trajectoires circulaires par rapport à un repère donné.

Notion de moment d'inertie

La position de centre d'inertie ne suffit pas pour déterminer les caractéristiques de mouvement d'un solide soumis à l'action des forces acquis sous l'action d'une impulsion extérieure dépend de la distribution des masses à l'intérieur du solide.
Pour tenir compte de l'influence de ce dernier critère dans le mouvement de rotation d'un solide on introduit une nouvelle caractéristique: le moment d'inertie.
Le mouvement d'inertie d'un système par rapport à un axe est par définition la somme du produit des parties ponctuels i par le carré de la distance de cette partie à l'axe.

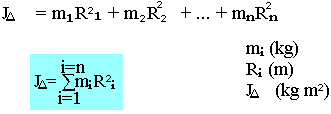
Exercice d'application 1

Soit à déterminer le mouvement de deux points matériel de masse respective m₁=4Kg et m₂=7Kg situer à 6Cm et à 2Cm de l'axe respectivement.
J = m₁R₁² + m₂R₂² = 4(6x10^-2)² + 7(2x10^-2)²
J = 1,75 x 10^-2 Kgm²

Exercice d'application 2

Déterminer le moment d'inertie d'un pendule simple de longueur 15Cm et de masse 3Kg
J = ml²
J = 3(15x10^-2)²
J = 6,75x10^-4 Kgm²

Théorème de Huygens

Le moment d'inertie d'un système de masse M par rapport à un axe de rotation quelconque est égal à son moment d'inertie par rapport à son centre d'inertie parallèle D augmenté du produit de la masse du système par le carré de la distance qui sépare les deux axes.
J_D = J_G + M.d²

Loi fondamentale de la dynamique

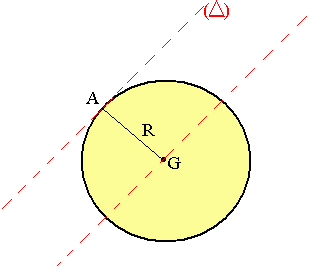
Soit à déterminer le moment d'inertie d'une circonférence de masse M de rayon R par rapport à un axe horizontal perpendiculaire au plan de la circonférence et passant par un point A de cette circonférence
J_D = J_G + Mr² or J_G = Mr²
J_D = Mr² + Mr²
J_D = 2Mr²

Remarque:

Pour un cerceau au circonférence pesant de masse M de rayon R. Pour un cylindre creux de masse M et de rayon R. Pour une poulie de masse M repartie sur sa circonférence de rayon R. J_G=M.R²

Pour un cylindre plan de masse M et de rayon R

Pour un disque plein de masse M et de rayon R

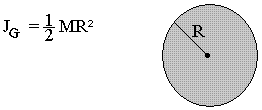
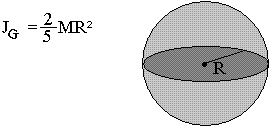
Pour un sphère pleine de rayon R de masse M