Onde progressive
Si on laisse tomber une goutte d'eau à la surface libre d'un liquide au repos, on observe qu'il naît au point de chute des rides circulaires qui s'agrandissent progressivement en s'éloignant de ce point ceci est dû à la propagation dans toutes les directions à la surface du liquide de la déformation créée au point de chute. La cause de la perturbation est appelée émetteur. La déformation qui se propage s'appelle onde progressive. Le point où la perturbation est créée s'appelle la source. L'environnement qui permet la propagation de l'onde est le milieu de propagation: Dans un milieu homogène une onde se propage à lui même vitesse et dans toutes les directions est la vitesse de propagation est donnée par la relation v=d/t.
La période T est la période posée à la source par l'émetteur.
L'équation ou l'élongation de la source est de la forme Ys=aSin(ωt+Þ)
On appelle longueur d'onde la distance parcourue par l'onde pendant une période de mouvement de la source.
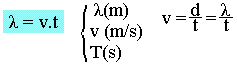
Lorsqu'une onde se propage dans la direction de la perturbation, elle est dite longitudinale. Et si elle se déplace dans une direction perpendiculaire à celle de la perturbation, elle est dite transversale.
Equation de l'onde en un point M du milieu de propagation
Considérons une corde fixée en O à un vibreur et passant par A par la gorge d'une poulie de masse négligeable. Cette corde est tendue à l'aide des masses marquées fixées de l’autre côté de la poulie.
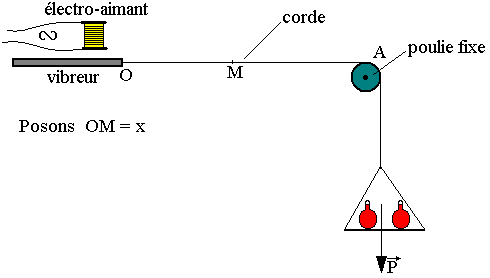
Le mouvement transversale appliqué à la source a pour équation Y0=aSin(ωt+Þ). Le point M reproduit le mouvement de la source O.
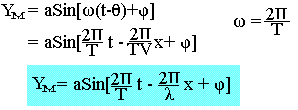
D'après cette équation l'onde en M vibre avec un double périodicité temporale T et spatial.
On montre que l'ébranlement créé en O se propage le long de la corde avec une vitesse ou une célérité.
v = c = (F/µ)½
F(N): tension de la corde
µ(Kg/m): masse linéaire (ou linéique) de la corde.
Pour deux points M1 d'abscisse OM1=x1 et M2 d'abscisse OM2=x2 en posant
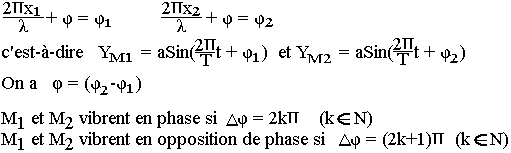
Remarque:
La célérité du son est donnée par la relation:

Interférence d'onde
Définition et exemple
On appelle interférence d'onde, le phénomène résultant de la superposition d'au moins deux ondes progressives de même nature et de même fréquence.
Pour que de telles ondes puissent interférées, elles doivent être cohérentes, c'est-à-dire que les fonctions mathématiques qui leur sont associées. Exemple: interférence d'onde mécanique à la surface de l'eau.
Une fourche munie de deux pointes est actionnée par un vibreur de pulsation ω. Les deux points très en S1 et S2 à la surface d'un liquide des ondes qui se propagent. On peut alors observer le phénomène résultant de la superposition de ces ondes.
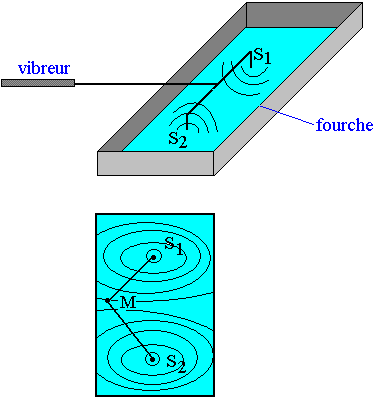
En éclairage normal on observe à la surface du liquide:
- Dans la zone située entre les sources S1 et S2 des lignes de crête en forme d'arc d'hyperbole: Ce sont des franges ou lignes d'interférences.
- En dehors de cette zone des rides circulaires qui s'agrandissent en s'éloignant de S1 et S2
On appelle champ d'interférence la zone située en S1 et S2 où des lignes stationnaires vibrent.
En éclairage stroboscopique les franges d'interférence sont de deux types: les franges au repos (ensembles de points ayant une amplitude nulle); des franges d'agitation maximales (ensemble des points vibrant avec une amplitude plus grande que celle des sources prises individuellement).
Etablissement de l'élargissement d'un point vibrant M
Considérons deux sources S1 et S2 d'équation:
![]()
Le point M situé à d1 de S1 et d2 de S2 a respectivement pour élongation comme si les sources vibraient seules.
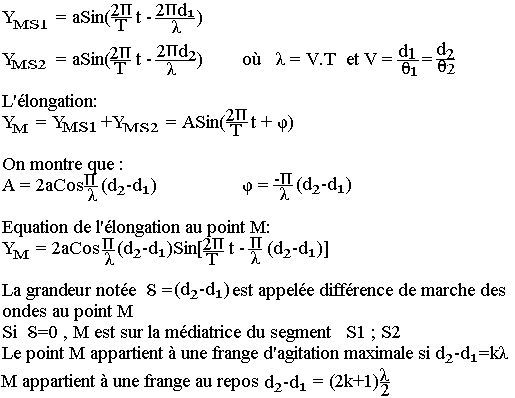
Les ondes stationnaires
On appelle ondes stationnaire le résultat de la superposition de deux ondes progressives synchrones se propageant dans la même direction mais en sens contraire mais en sens contraire dans le même milieu de propagation.
La corde de MELDE
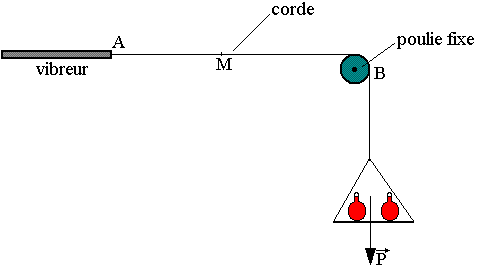
La corde de MELDE est une corde AB donc les extrémités B et A sont respectivement fixes et actionnées par vibreur de fréquence déterminée. La perturbation imprimée en A à la corde initialement au repos se propage le long de celle-ci; elle se réfléchit en B et rebrousse chemin. La corde est le siège des ondes l'une incidente et l'autre réfléchie. En tout point M de la corde et à tout instant la perturbation se propage à la vitesse C= (F/µ)½
En éclairage stroboscopique normale on observe sur la corde des fuseaux donc les renflements sont appelés ventre et les extrémités noeuds
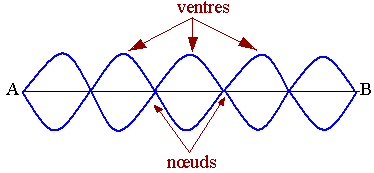
En éclairage stroboscopique la corde présente l'aspect d'une sinusoïde dont l'amplitude varie progressivement. La sinusoïde n'avance pas mais se déforme sur place d'où le nom d'onde stationnaire.
Analyse mathématique
Pour les commodités de travail, on considère le point B comme l'origine du repère
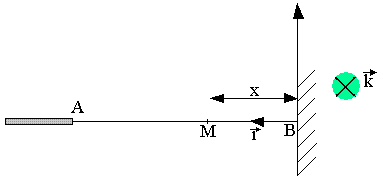
L'onde incidente qui arrive en B a pour équation yIB=aSinωt, l'onde réfléchie qui part de B est yRB telle que
YIB+YRB = 0
Pour le point M l'onde incidente y arrive avant d'atteindre l'origine.
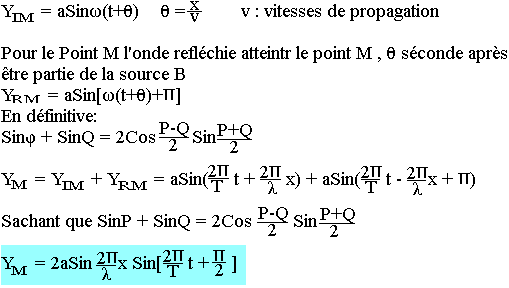
Le point M appartient à un noeud de vibration si son amplitude est nulle
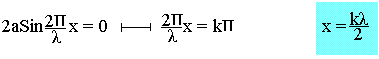
On montre que la distance entre deux noeuds consécutifs est
![]()
M appartient à un ventre de vibration si son élongation est maximale
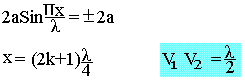
Si xA-xB=l (longueur de la corde)
Si A et B sont les noeuds de vibration
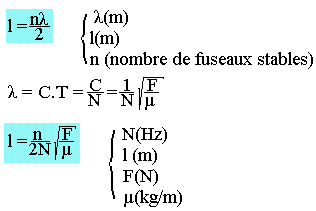
On montre également qu'on peut obtenir des ondes stationnaires sur onde AB donc l'extrémité B est libre ou mobile. L'expression de la longueur de la corde est
![]()
n (nombre de fuseaux stables)
Les interférences lumineuses
Expérience de la fente de YOUNG
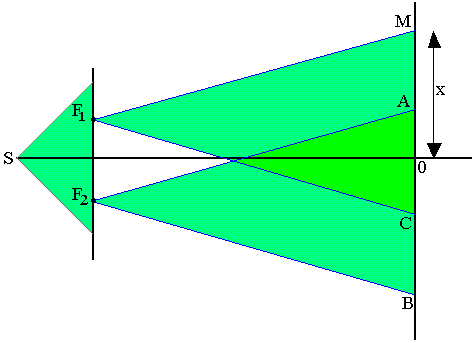
S est une source monochromatique (une seule longueur d'onde) F1 et F2 sont deux fentes sur une plaque opaque qui se comporte à cause de la diffraction de la lumière comme deux sources secondaires.
Lorsque S émet, les fentes F1 et F2 étant ouvertes, on observe sur les parties A et B de l'écran un éclairement uniforme. Sur la partie C on observe des bandes alternativement brillantes et obscures: ce sont des franges d'interférence. Ce phénomène se rapproche de celui des interférences mécaniques pour lesquels on avait un mouvement plus intense (ligne de vibration maximale) et l'immobilité (ligne au repos) ont ici une lumière intense (franges brillantes) et l'obscurité (frange sombre).
La différence de marche et notion d'interfrange
La différence de marche
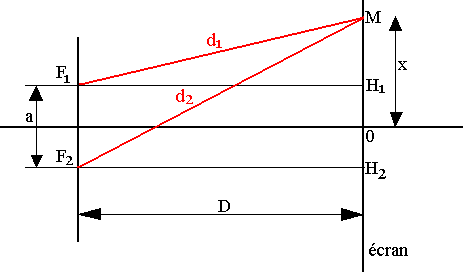
On appelle différence de marche la somme d2-d1=ax/D
d22 = F2H22+H2M2 = D2+(x+a/2)
d12 = F1H12+H1M2 = D2+(x-a/2)2
d22-d12 = [D2+(x+a/2)2]+[D2+(x+a/2)2] = (x+a/2)2-(x-a/2)2 = 2xa.
En posant d1+d2=2D on a:
d22-d12 = (d2-d1)(d2+d1) = (d2-d1)2D = 2ax
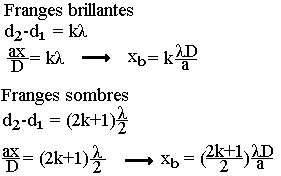
Interfrange
On appelle interfrange, la distance séparant les milieux de deux franges consécutives et de même nature.
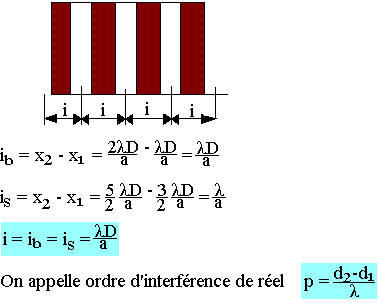
Pour une frange brillante p, est un entier.
Pour une frange sombre p est un demi-entier.
L'ordre d'interférence renseigne sur le numéro de la frange comptée à partir de la frange centrale brillante pour laquelle p=0
La lumière du soleil est blanche quant elle traverse un prisme elle se révèle être composée de plusieurs couleurs. Cette série de couleur est appelée spectre visible de la lumière blanche. L'interférence lumineuse en lumière blanche donne des franges multicolores. Toutefois la frange centrale brillante commune aux 7 radiations est unique et blanche, de part et d'autre on a un spectre cannelé.