Page 1 sur 5
Définitions et généralités
- Un réseau est un ensemble de conducteurs reliés entre eux et contenant en général des générateurs, des récepteurs et des résistances.
- Un noeud est un point du réseau où sont connectés plus de deux conducteurs.
- Une branche est une portion du réseau située entre deux noeuds.
- Une maille est un ensemble de branchement formant un circuit fermé qui ne passe qu'une fois par un noeud donné.
Dans les réseaux, le problème qui se pose est le suivant:
- Les résistances, les forces électromotrices, les forces contre électromotrices étant comme il faut déterminer les intensités des courants qui circulent dans chaque branche en grandeur et en sens
- Il y'a évidemment autant d'inconnue que de branchement que de branche il faut donc trouver les équations en nombre suffisant pour trouver les inconnues.
- Nous allons donc passer en revue les différentes méthodes d'étude et nous mettons chaque fois en relief leur qualité et leur défaut.
Lois de KIRCHOFF
Il en existe deux, celle relative aux noeuds et celle relatives aux maille.
Loi relative aux noeuds
Considérons un noeud A où passent des courants d'intensité i1, i2, i3, i4 et i5
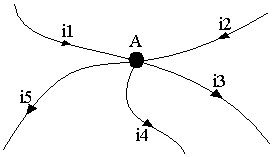
On a alors i1+i2=i3+i4+i5
Ainsi les différents courants entrant et sortant en un noeud sont liais par la relation
Somme de courants entrants = somme de courants sortants.
Loi relative aux mailles
La loi d'Ohm généralisée est valable ici et s'écrit
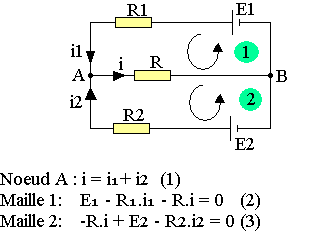
En prenant un circuit fermé A B on a:
La loi KIRCHOFF relative aux mailles s'écrit alors
Utilisation des lois de KIRCHOFF
Pour utiliser les lois de KIRSHOFF on procède de la manière suivante:
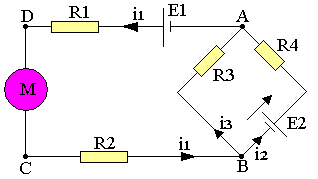
- Sur chaque branche on adapte un sens positif de mesure pour le courant, le plus vraisemblable et une valeur algébrique du courant. On écrit les lois relatives aux noeuds i1=i2+i3au noeud B
- On écrit ensuite la loi relative aux mailles pour le nombre convenables de maille indépendante en prenant sur chaque maille un sens de parcours arbitraire.
- R3i3+R4i2-E2=0
- On obtient ainsi un nombre d'équation linéaire permettant de calculer les intensités inconnues la résolution de ce système d'équation forme les valeurs algébriques des intensités.
Les valeurs positives signifient que le courant circule effectivement dans le sens choisi, s'il y'a pas de récepteur non polarisé, des valeurs négatives signifient que le courant circule dans le sens opposé.
Enfin s'il y'a des récepteurs non polarisés et si l'on trouve dans une branche contenant un tel récepteur une intensité négative, il faut recommencer les calculs en inversant le sens de cette intensité. Le récepteur non polarisé s'opposant toujours à l'intensité.
Si en fin de calcul on trouve dans cette branche une intensité positive tout va bien.
Si on trouve encore une intensité négative, cela signifie que la ddp aux bornes du récepteur est insuffisante pour faire fonctionner celui-ci: aucun courant ne traverse dans la branche et on peut le supprimer.
Le calcul est terminé lorsque toutes les intensités sont positives dans toutes les branches contenant des récepteurs non polarisés.
Exemple
Nous nous proposons d'appliquer les lois de KIRSHOFF au réseau suivant:
Concours d'entrée aux grandes écoles
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale