Généralités
Les courants alternatifs sinusoïdaux usuels ont des fréquences suffisamment faibles pour que l'approximation des états stationnaires soit valable. Tout cela revient donc à écrire les mêmes lois qu'en courant continu en tenant compte en plus des forces électromotrices d'induction qui peuvent prendre naissance dans les inductions sinusoïdale du flux magnétique.
Différence de potentielle aux bornes des éléments d'un circuit
Résistance morte
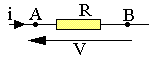
V = VA-VB = Ri
Inductance
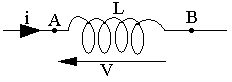
e = -dØ/dt = -Ldi/dt
V = VA - VB = Ldi/dt
Condensateur
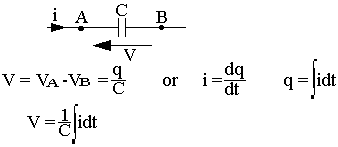
Régime forcé d'un circuit en courant alternatif sinusoïdal: méthode de résolution
On considère le circuit RLC ci-dessous
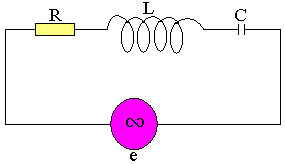
Le générateur délivre une force électromotrice alternative de la forme e=EmCosωt.
Ainsi en écrivant la loi d'Ohm aux bornes de chacun des éléments on obtient l'équation différentielle permettent de calculer l'intensité du courant i à l'instant t, c'est-à-dire:
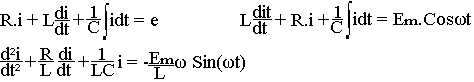
La solution générale de l'équation sans second membre est telle que i=e-Rt/2Lf(t) et la solution générale de l'équation avec second membre est telle que i(t)=e-Rt/2Lf(t)+ACosωt+BSinωt. Au bout d'un temps plus ou moins bref i tend vers la valeur i=ACosωT+BSinωt. Dans ce cas la solution cherchée sera donc de la forme i=ImCos(ωt+þ). Il s'agit donc de déterminer Im et þ par la méthode symbolique.
Méthode symbolique
Elle est fondée sur la loi des membres complexes. Soit une fonction sinusoïdale y=aCos(ωt+þ). On peut lui associer la fonction telle que z=y+jx avec j2=-1
z = a[cos(ωt+þ)+jSin(ωt+þ)] = aej(ωt+þ)
Ainsi à l'intensité i=ImCos(ωt+þ) on associe I=Imej(ωt+þ) et à la force électromotrice sinusoïdale e=EmCosωt on associe la partie imaginaire E=Emejωt.
Le facteur ejωt se trouvant en facteur commun dans tous les termes, on le met puisqu'on considère le régime forcé.
On appelle donc:
- Intensité complexe: la grandeur I=Imejþ
- Force électromotrice complexe: la grandeur E=Em
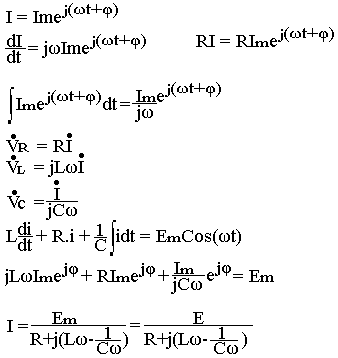
La quantité Z=R+j(Lω-1/Cω) homogène à une résistance est appelée impédance complexe du circuit.
La partie imaginaire souvent notée X est appelée réactance.
L'impédance Z du circuit exprimée en ohm s'écrit Z=[R2+(Lω-1/Cω)2]½.
Plus simplement les impédances complexes sont:
- Pour une résistance ZR=R
- Pour une inductance ZL=jLω
- Pour une capacité ZC=-j/Cω=1/jCω
Ainsi pour des impédances Z1, Z2 et Z3 montrées en série. On a Z=Z1+Z2+Z3 et pour ces impédances montées en parallèle, on a: 1/Z=1/Z1+1/Z2+1/Z3
On admet donc que la loi d'Ohm en courant alternatif sinusoïdale est V=Z.I
Influence de la fréquence
- Pour une inductance ZL=jLω
- En basse fréquence (ω→0) une inductance se comporte comme un court-circuit.
- En haute fréquence (ω→ l'infini) une inductance se comporte comme un circuit ouvert.
- Pour un condensateur ZC=1/jCω
- En basse fréquence (ω→0) un condensateur se comporte comme un circuit ouvert.
- En hâte fréquence (ω→ l'infini) il se comporte comme un court-circuit.