Diagramme de Bode
On entend par diagramme Bode un ensemble de deux courbes qui permettent de comprendre le comportement de quadripôle sur une plage étendue de fréquence.
- La courbe représentant les variations du gain en fonction de la fréquence G=50Log|T|
NB: On peut aussi présenter en fonction des pulsations - La courbe représentant les variations de l'argument þ=arctg(b/a)
Calcul du logarithme décimal
On doit connaître les valeurs remarquables du logarithme décimal. Elle sont dénombrées par ordre d'importance suivant la représentation ci-dessous
Log(a+b) = Loga + Logb
Loga/b = Loga - Logb
Logan = nLoga
Log1/b = Log1 - Logb = -Logb
Remarques:
- Dans la pratique si Gv(dB)=0 h=T=1 d'où le quadripôle est dit adaptateur d'impédance
- Si GV(dB)<0 ; H<1 ou T<1 Le quadripôle dit atténuateur d'information.
- Si GV(dB)>0 ; H>1 ou T>1 Le quadripôle est dit applicateur d'information
Notion de la bande passante
La bande passante pour un amplificateur est l'intervalle dans lequel la transmission de puissance dans lequel la transmission de puissance est maximale d'où le gain est maximale dans cet intervalle et il est appelé G0. Cependant la bande passante à -3dB est l'intervalle dans lequel le gain maximal G0 est diminué de -3dB ou GV=G0=-3dB. De ce fait les deux fréquences limites sont appelés fréquence de coupure inférieur et fréquence de coupure supérieure
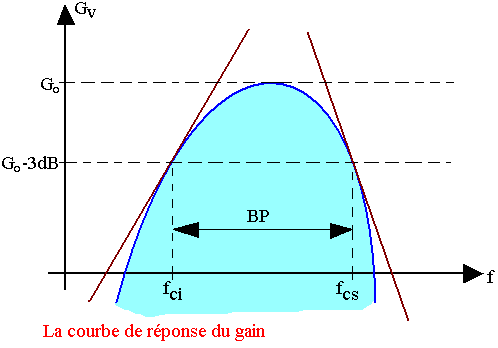
Détermination du gain à -3db
A partir de la figure de la bande passante, on peut déterminer le gain à -3dB en identifiant les fréquences fci et fcs. De ce fait si I est la transmitance d'un quadripôle T0 sa valeur maximale, on aura donc le gain G=20Log|T| et G0=20Log|T0|. Par ailleurs dans l'intervalle B la condition de déterminer le gain à -3dB
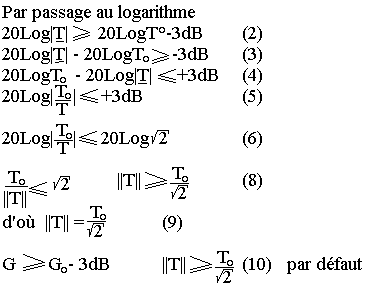
On remarque bien que la diminution du gain à -3dB correspond à une atténuation du module de la fonction de transfert par rapport à sa valeur maximale T0. De plus la condition (10) permet également de déterminer les fréquences de coupure à -3dB en résolvant les équations ci-dessous
aX4 + bX2 + c = 0
a'X2 + b'X + d = 0
Pour cela on pose X2=x ; X4=x2
Facteur de mérite
Il est noté M est représente le produit de la bande passante et de la valeur maximale de la fonction de transfert M=B.T0
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale