Notions fondamentales
Un signal est défini comme le support physique de l'information, exemple: le signal sonore représente les fluctuations de la pression de l'aire qui est transmise à l'oreille.
Mathématiquement un signal est représenté par une fonction d'une ou plusieurs variables généralement cette variable est le temps.
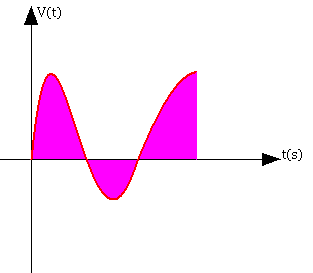
Ici le signal est fonction de deux variables, une tension en fonction du temps.
Une image de télévision est fonction de l'espace et du temps.
Classification des signaux
La variable indépendante de la représentation mathématique des signaux peut être continue ou discrète, de même l'amplitude du signal peut être continue ou discrète.
Exemple:
[1; 3] dans R, il y'a une infinité de nombre réels.
[1; 3] dans N, il existe 3 entiers naturels 1, 2, 3 (on peut les compter)
- Signaux analogiques:
- Variables continues
- Amplitude continue
- Signaux échantillonnés:
- Variables discrètes
- Amplitude continue
- Signaux quantifiés:
- Variables continues
- Amplitude discrète
- Signaux numériques:
- Variables discrètes
- Amplitude discrète
Nous aurons besoin des dispositions électriques qui peuvent convertir un signal analogique à un signal numérique utilisable par les appareils informatiques On les appelle les CAN: ADC (Analog to Digital Converter).
Nous avons aussi besoin d'un convertisseur numérique analogique CNA pour permettre de restituer le signal d'origine.
La conversion analogique numérique est l'opération la plus difficile, parce que il faut tenir compte de l'évolution du signal analogique car celui-ci n'est pas figé.
Cette opération se passe en 4 étapes qui sont:
- L'échantillonnage
- La quantification
- La compression
- Le codage
Signaux numériques
Un signal discret est une suite de valeurs réelles complexes, s'il est formé de valeurs réelles , il sera dit réel, s'il est formé de valeur complexe il sera dit complexe.
Un signal numérique est un signal discret et donc l'amplitude est quantifiée.
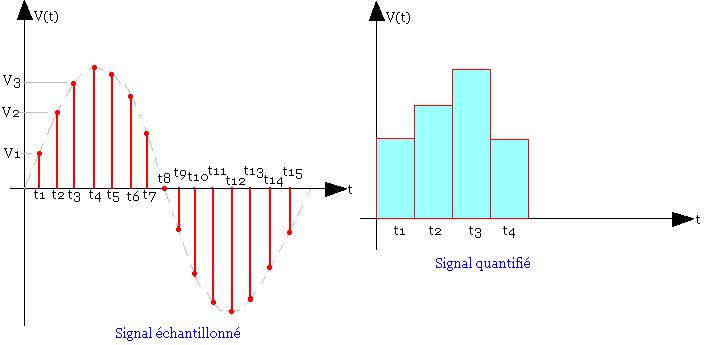
Quantifié: un nombre fini de valeurs.
Echantillonné: un nombre fini des instants
Notation:
Nous utilisons deux types de notation : x(k), k appartient à IN ou x(k∆t). ∆t est la période d’échantillonnage
Remarque :
Si ∆t =1
X(k) = x(k∆t)
Signaux élémentaires: (numérique)
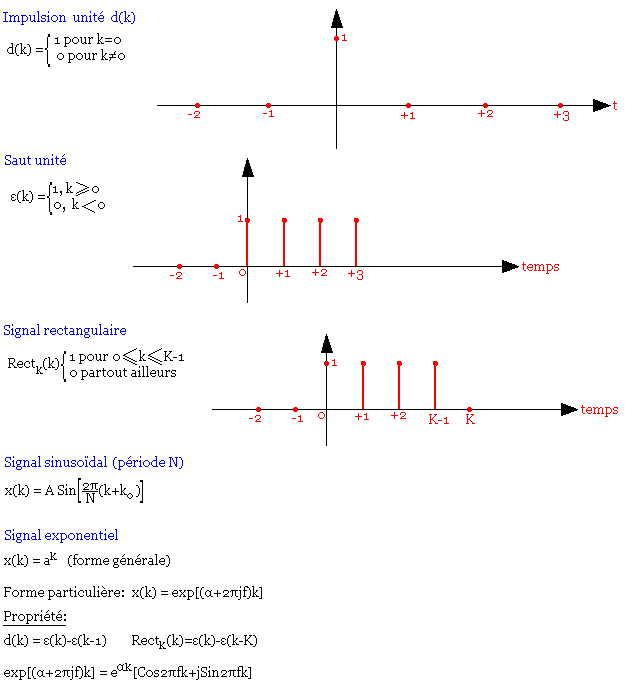
Notes:
Codage: Tous les échantillons doivent avoir le même nombre de bit pour être représenté, les "1" logiques et les "0" logiques doivent être représentés de la même manière quelque soit l'échantillon.
Compression: Réduction de la quantité de l'information à transmettre.
Démonstration
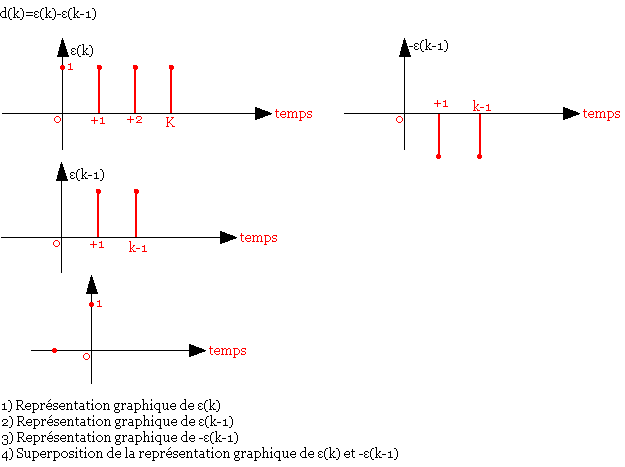
Signal périodique
On dit qu'un signal est périodique de période K si x(k)=x(k+K).
On définit également un signal à durée limitée. Un signal défini pour un nombre fini d'échantillon est appelé signal à durée limité. Le nombre de K représente alors la durée ou encore la longueur d'un tel signal.
- La puissance moyenne d'un signal numérique est égale à:
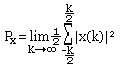
- L'énergie est égale à:
![]()
Opérations élémentaires sur les signaux
- Somme: z(k) = x(k)+y(k)
- Produit: z(k) = x(k).y(k)
- Décalage: z(k) = x(k-k0)
Système causal
Il est caractérisé par le fait que la réponse ne précède jamais l'excitation.

Opération:
Si x(k)=0 pour k<k0 alors y(k)=0 pour k<k0
Système linéaire
S[ax1(k)+bx2(k)] = aS[x1(k)] + bS[x2(k)]
Supposons que y1(k)=S[x1(k)] et y2(k)=S[x2(k)]
x(k)=ax1(k)+bx2(k)
y(k)=S[x(k)]=ay1(k)+by2(k)
Equation aux différences
C'est la version discrète des équations différentielles linéaire caractérisant les systèmes linéaires analogiques.
a0(k)+a1(k)y(k-1)+a2(k)y(k-2)+...+aN(k)y(k-IN)=b0(k)x(k)+b1(k)x(k-1)+b2(k)x(k-2)+...+bM(k)x(k-M)
![]()
Dans le cas où les cœfficients an(k) et bn(k) sont indépendantes de k, nous avons une équation linéaire à cœfficient constant.
On peut résoudre par rapport au kième échelon.
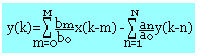
Exemple1:
y(k) = x(k)-ay(k-1)
Conditions initiales
y(k) = 0 pour k<0
x(k) = ε(k)
D'une manière itérative on obtient
y(0) = x(0)-ay(-1) = 1-0 = 1
y(1) = x(1)-ay(0) = 1-a
y(2) = x(2)-ay(1) = 1-a(1-a) = 1-a+a2
y(3) = x(3)-ay(2) = 1-a(1-a+a2) = 1-a+a2+a3
y(4) = x(4)-ay(3) = 1-a(1-a+a2-a3) = 1-a+a2-a3+a4
.
.
.
y(k) = x(k)-a(k-1) = 1-a+a2-a2-a3+a4+...+(-1)kak
y(k) est une suite géométrique de premier terme y(0)=1 de dernier terme y(k)=(-1)kak la raison est q=-a
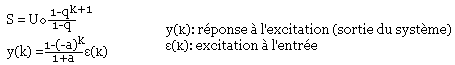
Exemple2:
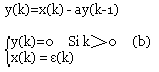
Relation entre y(k-1), x(k) et y(k).
Nous avons y(k) = x(k)-ay(k-1)
y(k-1) = [x(k)-y(k)]a-1
En utilisant une approche itérative on obtient:
y(0) = [x(1)-y(1)]a-1 = a-1
y(-1) = [x(a)-y(a)]a-1 = a-1(1-a-1) = a-1-a-2
y(-2) = [x(-1)-y(-1)]a-1 = a-1[-(a-1-a-2)] = a-2-a-3
y(-3) = [x(-2)-y(-2)]a-1 = a-1[-(-a-2+a-3)] = a-3-a-4
y(-4) = [x(-3)-y(-3)]a-1 = a-1[-(a-3-a-4)] = -a-4+a-5
.
.
.
y(k) = [x(k+1)-y(k+1)]a-1 = (-1)k-1(ak-ak-1)ε(-k)
Remarque1:
Cette réponse : y(k) = (-1)k(ak-ak-1)ε(-k) est tout à fait différente de la première. Avec la même excitation et pour des conditions initiales différentes nous obtenons des solutions différentes.
Remaque2:
On peut résoudre une équation par la méthode itérative ou par la méthode analytique. La méthode analytique est celle utilisée pour une équation différentielle à cœfficient différent à savoir:
- Recherche de la solution générale de l'équation homogène:
- Recherche de la solution particulière de l'équation avec second membre (b)
- La solution générale de l'équation est égale à la somme de a et b
- La solution recherchée s'obtient en appliquant les conditions initiales.
