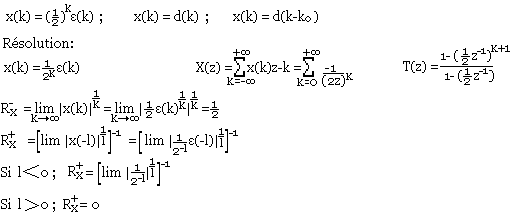Transformation directe
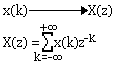
La transformation en Z est une opération bilatérale car la sommation passe de moins l'infini à plus l'infini. Pour un signal causal on définit la transformation unilatérale suivante.
Région de convergence
L'ensemble des Z pour lequel la série ci-dessous est convergente est appelé région de convergence. Pour trouver cette région de convergence on peut utiliser le critère de CAUCHY sur la convergence d'une série de puissance.
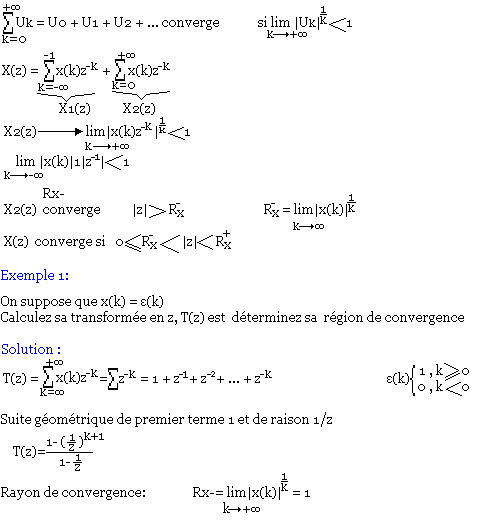
Pour X1(z) avec un changement de variable l=-k. On peut montrer de la même manière que X1(z) converge lorsque |z| est inférieure ou égale à Rn+ avec
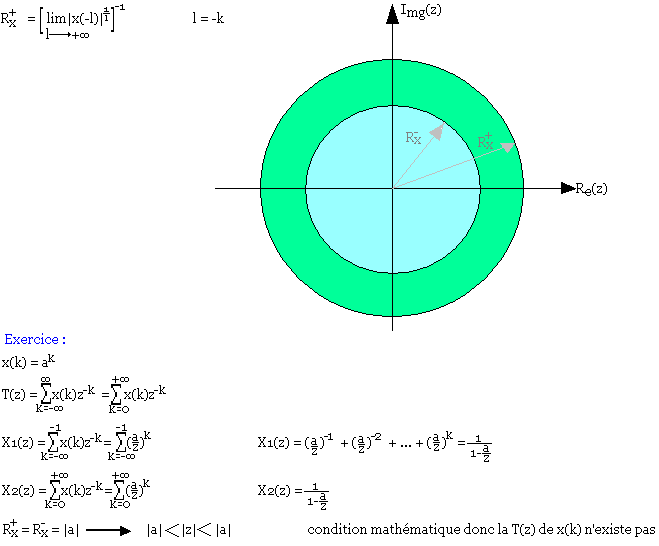
Transformation inverse
On peut calculer la transformée en z inverse de plusieurs manières:
- Calcul des résidus
- Développement en série de puissance
- Développement par division
Utilisation du théorème de CAUCHY.
Relation entre la transformée en z et la transformée de FOURRIER
D'après la définition de la transformée en z nous avons:
La transformée de FOURRIER d'un signal est la transformée en z de ce signal évalué sur un cercle de rayon unité (rayon=1).
En conclusion la transformée en z est une généralisation de la transformée de FOURRIER.
Exercice d'application:
Déterminez la transformée en z et la région de convergence pour les signaux suivants:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale