Généralités
Lorsque la complexité d'un problème s'accroît, il devient nécessaire d'utiliser les sous-programmes pour alléger la tâche. Ces sous-programmes sont les procédures et les fonctions. De façon générale les sous programmes nous permettent:
- D'éviter de copier un segment de code plusieurs fois dans un même algorithme.
- De décomposer un grand problème en petit module ou sous problème, chacun effectuant une tâche bien précise. Les modules peuvent être écrites par plusieurs personnes de façon indépendante.
- De constituer une bibliothèque sous-programme.
Définition
- Le sous-programme est une suite d'instruction ordonnée que la machine n'exécute lorsque c'est nécessaire
- La procédure est un sous programme qui peut calculer et mettre à la disposition de l'utilisation plusieurs valeurs
- La fonction est un sous-programme qui calcule et met à la disposition de l'utilisateur une valeur unique. La valeur calculée est mise à la disposition de l'utilisateur par l'intermédiaire du nom de la fonction qui est une variable d'un type donné: celui de la valeur calculée.
Syntaxe des sous-programmes
Procédure: nom (liste des paramètres)
déclaration
début
corps de la procédure
fin
Exemple:
Ecrire une procédure qui prend en paramètre deux nombres "a" et "b", qui calcule la somme et la moyenne de ces nombres
Algorithme: somme(A, B, S, M: réel)
debut
S←A+B
M←S/2
fin
Syntaxe d'une fonction
Fonction: nom (liste des paramètres): type
déclaration
debut
corps de la fonction
nom_de_la_foncton←valeur_calculée
fin
Exemple:
Ecrire une fonction qui prend en paramètre deux nombres et renvoie la moyenne de ces nombres.
fonction moyenne(A, B: réel):réel
var m: réel
debut
m←(A+B)/2
moyenne←m
fin
Passage de paramètres
On distingue les paramètres effectifs et les paramètres formels.
- Un paramètre formel est un paramètre utilisé dans la définition d'un sous programme.
- Un paramètre effectif ou réel est un paramètre utilisé lors de l'appel d'un sous-programme.
Un sous-programme peut avoir trois types de paramètre:
- Les paramètres d'entrée fournissent les données au sous-programme. Exemple: A et B étaient les paramètres d'entrée précédemment)
- Les paramètres de sortie: les paramètres de sortie contiennent les résultats à la fin du déroulement du sous-programme. Exemple: S et M était les paramètres de sortie précédemment)
- Les paramètres d'entrée-sortie jouent deux rôles: Il jouent le rôle de paramètre d'entré et celui de paramètre de sortie.
Introduction à l'analyse descendante
Soit un travail T décrit par un énoncé E, l'analyse descente du travail T consiste à trouver une décomposition de l’énoncer E en une suite d’énoncer E0, E1, ..., En-1 tel que la décomposition obtenue soit élémentaire.
La réalisation des travaux associées T0, T1, ..., Tn-1 réalise le travail T.
L'arbre hiérarchique ou arborescence hiérarchique correspondant respective à l'énoncé E et le travail T se présente comme suite:
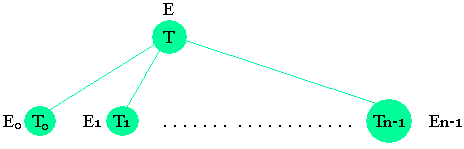
Chaque Ei ou Ti peut également être décomposé:
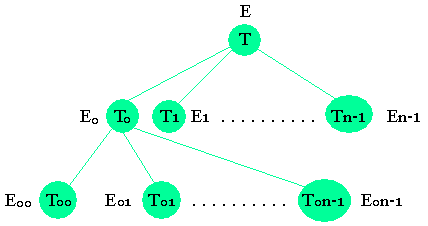
La décomposition s'arrête lorsque l'on obtient des énoncés pouvant être réalisés simplement à l'aide d'action élémentaire.
Après la décomposition chaque énoncé peut être réalisé par un algorithme ou un sous-programme indépendant. L'enchaînement approprié de ces algorithmes ou sous-programme permet de réaliser le travail T.
Application
Problème 1
Ecrivons un algorithme qui permet de calculer Cpn avec P inférieur ou égal à n. Ce problème peut être décomposé en trois modules comme suite:
- La lecture de "p" et "n" avec les conditions suivantes: n supérieur ou égale à 0; p supérieur ou égale à 0; p est inférieur ou égale à n.
- Le calcule de la factoriel d'un nombre
- Le calcul du quotient A/B*C
L'arborescence hiérarchique de ce problème est sous la forme:
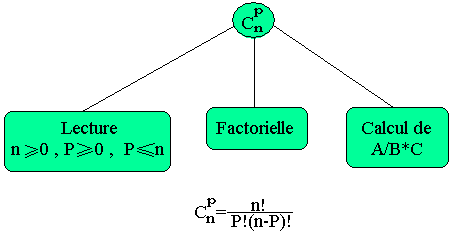
Résolution:
procédure: lecture(x, y: entier)
debut
répéter
lire(x)
jusqu'à x>=0
répéter
lire(y)
jusqu'à y>=0 et y<=n
fin
fonction: factorielle(m:entier):entier
var i, fact: entier
debut
si m=0 alors
fact←1
sinon
fact←1
pour i=1 à m faire
fact←fact*i
fin pour
fin si
factorielle←fact
fin
fonction: combinaison(a, b, c: entier):entier
var z: entier
debut
z←a div(b*c)
combinaison←z
fin
Algorithme: combinaison_P_N
var n, P, R, A, A, B, C: entier
debut
lecture(n,P)
A←factorielle(n)
B←factorielle(p)
C←factorielle(n-P)
R←combinaison(A,B,C)
écrire(R)
fin
Problème 2
Ecrire un algorithme qui permet de résoudre une équation du second degré de la forme ax2+bx+c=0 avec a différent de zéro.
Arborescence:
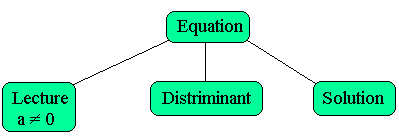
Procédure: lecture(a,b,c: réel)
debut
répéter
lire(a)
jusqu'à a#0
lire(b,c)
fin
Fonction discriminant(a, b, c: réel):réel
var d: réel
debut
d←b**2-4*a*c
discriminant←d
fin
Procédure: solution(d:réel)
var x0, x1, x2: réel
debut
si d<0 alors
écrire('pas de solution')
sinon
si d=0 alors
x0← -b/2
écrire('la solution est x0= ',x)
sinon
x1←(-b-sqrt(d))/2*a
x2←(-b+sqrt(d))/2*a
écrire('les solutions sont: ', x1, x2)
fin si
fin si
fin
Algorithme: équation
var dit, a, b, c: réel
debut
lecture(a,b,c)
det←discriminant(a,b,c)
solution(det)
fin
NB: "sqrt" permet d'avoir la racine carrée d'un nombre
