Exemple d'algorithme
Algorithme 1
Ecrire un algorithme qui permet de lire un entier "n" strictement positif et qui calcule la somme des "n" premier nombres positifs.
1) Algorithme
1a: somme
var N: entier
S: réel
debut
répéter
lire(N)
jusqu'à N>0
S←N*(N+1)/2
écrire('la somme de ',n,'premiers termes est: ,'S)
fin
Ici on a 3 opérations fixes
2) Algorithme
1b: somme
var n, i, S: entier
debut
écrire('Entrez un entier positif')
lire(x)
tant que n<=0 faire
écrire('Veuillez ressaisir votre nombre')
lire(x)
fin tant que
S←0
pour i=1 à n faire
S←i+S
fin pour
écrire('la somme des,'n', premier nombres positifs est ,'S)
fin
Ici on a n opération qui vont varier en fonction de n
Algorithme 2
Ecrire un algorithme qui permet de lire un entier "n" strictement positif et qui affiche tous les multiples de 3 inférieurs ou égaux à "n"
1) Algorithme 2a: multiple 3
var i, n: entier
debut
répéter
lire(n)
jusqu'à n>0
pour i=1 à n faire
si imod(3)=0 alors
écrire(i)
fin si
fin tant que
fin
2) Algorithme 2b: multiple 3
var i, n: entier
debut
répéter
lire(n)
jusqu'à n>=0
i←1
tant que i<=n faire
si imod3=0 alors
écrire(i)
fin si
i←i+1
fin tant que
fin
Efficacité et complexité d'un algorithme
Dans l'algorithme 1a, on a fait n additions.
Dans l'algorithme 1b, on a fait 3 opérations (une addition, une multiplication et une division)
Dans l'algorithme 2a, on a fait 2n+3 comparaisons, et n+1 opérations.
Des algorithmes produisant les mêmes résultats peuvent être très différent du point de vu des principes utilisés et du point de vu principes utilisés et du temps nécessaire pour obtenir les résultats.
On dit qu'un algorithme a, est plus efficace qu'un algorithme b si l'algorithme a fait bon usage des ressources de temps de traitement et mémoire par rapport à b. La mesure de l'efficacité d'un algorithme s'effectue en utilisant les notions de complexité théorique.
La complexité pratique (Tn)
C'est la mesure précise du temps et de la taille mémoire nécessaire à l'exécution d'un algorithme. Tn: Temps d'exécution
Complexité théorique
C'est un ordre de grandeur des coûts théoriques indépendants des conditions pratiques l'exécution (c'est une généralisation de la complexité pratique).

Exercice 2:
Calculer la complexité théorique de l'algorithme qui effectue la multiplication de deux matrices.
Pour des données de même taille le temps d'exécution peut être fonction de la valeur des données dans ce cas on définit deux types de complexité:
- La complexité max: Elle s'obtient avec les données les plus défavorables.
- La complexité min: Qui s'obtient avec les données les plus favorables.
La recherche dans un vecteur
Recherche séquentielle linéaire
Il s'agit de rechercher un élément dans un vecteur en effectuant un parcours séquentiel. La fonction correspondante est la suivante.
fonction recherche_sequentielle(V: vecteur, n, val, pos: entier): booléen
debut
i←2
tant que i<=N et val≠V[1] faire
i←i+1
fin tant que
si val=V[i] alors
recheche-sequentielle ← vraie
pos ← i
sinon
recherche-sequentielle ← faux
fin si
fin
Temps favorable (Tn)
TN=3TC
vals = 7
|
V : |
|
Temps défavorable (TD)
val = 7
|
V : |
|
TN = 5Ta+13TC = (n-1)Ta+(2n+1)TC
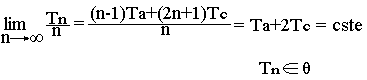
Recherche séquentielle avec sentinelle
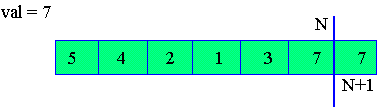
fonction recherche_sequentielle(V: vecteur, N, val, pos: entier): booleen
var i: entier
debut
V[N+1] ← val
i ← i+1
fin tant que
si i<=N alors
recherche_sequentielle ←- vraie
pos ← i
sinon
recherche_sequentielle ← faux
fin si
fin
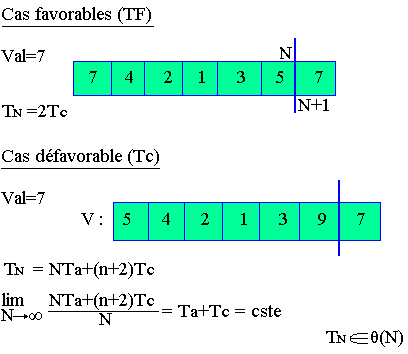
Recherche dichotomique
La recherche dichotomique suppose que le vecteur dans lequel on recherche une valeur "val" donnée est triée. Supposons que le vecteur est trié dans l'ordre croissant. Soit "min" et "max" les valeurs minimales et maximales de l'ensemble des indices du vecteur V. Le principe de la recherche dichotomique est le suivant:
- Calculer le milieu
mil = (min+max)/2 - Si V du milieu = val V[mil]=val alors on arrête la recherche car on a trouvé "val".
- Si V[mil]>val alors on continue la recherche dans la partie de V donc les indices varies entre "min" et "mil".
- Si V[mil]<val alors on continue la recherche dans la partie de V donc les indices varies entre "mil" et "max"
- Temps qu'on n'a pas trouvé val reprendre toute ces actions à partir de la première jusqu'à l'obtention d'un intervalle de recherche de taille "1".
S'il n'y a pas toujours égalité alors la valeur recherchée n'existe pas dans le vecteur.
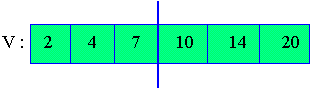
fonction rech(V: vecteur, n, val, pos: entier): booléen
var, mil, min, max: entier
trouve: booléen
debut
min ← 1
max ← n
trouve ← faux
tant que (min < max) et (non trouve) faire
mil ← (min+max)div2
si val < V[mil] alors
max ← mil
sinon
si val > V[mil] alos
mil ← mil+1
fin si
trouve ← val=V[mil]
fin tant que
rech ← trouve
fin
Les algorithmes simples de tri
Trier un ensemble de n informations consiste à classer ces fonctions selon certains critères (ordre croissant, ordre décroissant, ordre alphabétique)
Le tri sélection
La procédure correspondante est la suivante
procédure tri_selection(V: vecteur, n: entier)
var i, j, aux, pos: entier
debut
pour i=1 à n-1 faire
pos <-- i
pour j=i+1 à n faire
si V[pos] > V[j] alors
pos ← j
fin si
fin pour
aux ← V[pos]
V[pos] ← V[i]
V[i] ← aux
fin pour
fin
Exercice:
Réécrire cet algorithme en remplaçant la boucle "pour" par la boucle "répéter" et par la boucle "tant que".
Le tri par insertion
La procédure correspondante est la suivante:
procédure tri_insertion(V: vecteur, n: entier)
var i, j, x: entier
debut
pour i=2 à n faire
j ← i-1
x ← V[i]
tant que V[j]>x et j>0 faire
V[j+1] ← V[j]
j ← j-1
fin tant que
V[j+1] ← x
fin pour
fin
Exercice:
Réécrire cette procédure en remplaçant la boucle "tant que" par la boucle "répéter" et la boucle "pour" par "tant que".
Le tri par échange ou tri bulle
La procédure correspondante est la suivante:
procédure tri_bulle(V: vecteur, n: entier)
var i, aux: entier
T: booléen
debut
répéter
T ← vraie
pour i=1 à n-1 faire
si V[i]>V[i+1] alors
aux ← V[i]
V[i] ← V[i+1]
V[i+1] ← aux
T ← faux
fin si
fin pour
jusqu'à T {T=vrai}
fin
Exercice:
Réécrire cet algorithme en remplaçant la boucle "répéter" par la boucle "tant que"
