Vecteurs et points du plan
Vecteurs
Soit (A, B) un couple de point, t la translation transformant A en B. L'ensemble des couples (M, N) où N est l'image de M par t est le vecteur AB.
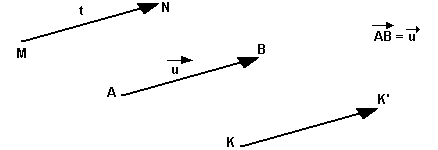
On appelle plan vectoriel l'ensemble de tous les vecteurs du plan.
Tout vecteur a une infinité de représentant.
Propriété fondamentale
Pour tout point O et tout vecteur, il existe un et un seul point M tel que vecteur de Om égal au vecteur u.
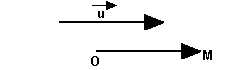
Propriété:
Les énoncés suivants sont équivalents:
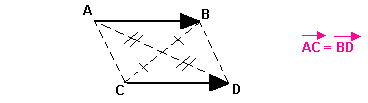
- Les vecteurs AB=CD signifie ABCD est un parallélogramme.
- [AD] et [CB] ont même milieu.
Direction, sens et normal d'un vecteur
On appelle norme de u la distance AB où (AB) est un représentant du vecteur u.
Propriété:
Il existe un et un seul vecteur ayant une direction donnée, un sens donné et une norme donnée.
Calcul vectoriel
Somme des vecteurs
Soit u et V des vecteurs. A, B, C des points tels que AB=u et BC=V, on pose u+V=AC
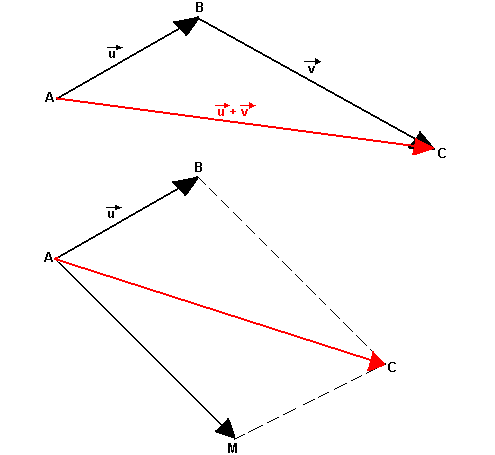
Relation de CHASLES
Pour tout point A, B, C
![]()
Inégalité triangulaire
Pour tout vecteur u et v on a:
![]()
Bases et repères
Base de V
Coordonnées d'un vecteur
Soit i et j 2 vecteurs non colinéaires.
Pour tous vecteur u il existe un vecteur et un seul couple de nombre réel (x; y) tel que u=xi+yj
Deux vecteurs sont colinéaires (u; v) dans les 2 cas suivants:
- Lorsque l'un d'eux au moins est nul.
- Lorsqu'ils ont même direction.
Soit u et v 2 vecteurs. Les vecteurs u et v sont colinéaires si et seulement si il existe un nombre réel λ.
Vecteur directeur d'une droite
On appelle vecteur directeur d'une droite (D) tout vecteur non nul u ayant même direction que (D).
On dit que (D) est dirigé par u
Tous couple (i; j) de vecteur non colinéaire est appelé base de V, est l'ensemble de vecteur du plan.
Soit (i; j) et u un vecteur; le seul couple non réel (x; y) vérifient u=xi+yj, est appelé couple de coordonnée de u dans la base (i;j)
Propriété:
Soit (i; j) une base de V, λ un nombre réel u et v 2 vecteurs.
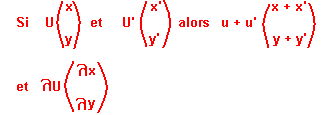
Base orthonormée
Deux vecteurs sont orthogonaux si leur direction est perpendiculaires ou si l'un au moins est nul.
Une base est dite orthonormée lorsqu'elle est constituée de 2 vecteurs unitaires orthogonaux.
(i, j) est orthonormé lorsqu'elle est constituée de 2 vecteurs unitaires orthogonaux (i,j) orthonormées si vecteur i est perpendiculaire au vecteur j, et ||i||=||j|=1
Expression de la norme dans une base orthonormée
Soit u (; y) dans une base orthonormée, on a:
![]()
Déterminant de 2 vecteurs
Soit (i; j) une base de V, u(x; y) et u(x'; y’) 2 vecteurs.
On appelle déterminant de (u; u’) relativement à la base (i; j) le nombre réel:
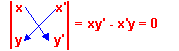
Théorème:
Soit (i; j) une base de V 2 vecteurs sont colinéaire si et seulement si leur déterminant est nul.
