La cotation est une opération qui consiste à indiquer sur le dessin d'une pièce toutes les dimensions qu'il faut connaître pour la fabriquer, chacune de ces dimensions est une cote.
Les cotes sont les dimensions réelles de l'objet
Règles générales
Certaines règles doivent être respectées pour une bonne cotation. Pour inscrire une côte, on utilisera un vocabulaire tel que:
- Ligne d'attache ou de rappel
- Les lignes de cote
- Les flèches
- Les cotes
- Place et orientation des chiffres
Ligne d'attache ou de rappel
Ce sont des traits fins tracés aux extrémités du segment à coter et perpendiculaires à ces segments. Elles doivent légèrement dépasser les lignes de cote.
Les lignes de cote
Ce sont des traits fins parallèles aux segments à coter et reliant les lignes d'attache. Elles sont placées à environ 8mm du trait du dessin
Les flèches
Elles se placent aux extrémités des lignes de cote et peuvent être disposées nez à nez ou dos à dos.
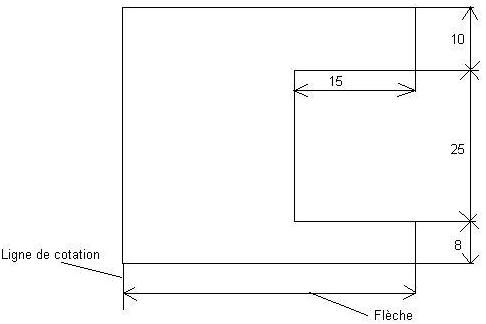
En cotation on indique les dimensions réelles du dessin et non pas les dimensions sur le dessin:
- L'unité employée est le millimètre mais on ne va jamais l'indiquer
- 2 lignes de cote ne doivent jamais se couper. voir figure A
- Une ligne d'attache ne doit jamais couper une ligne de cote. Voir figure B
- Dans certains cas un trait du dessin peut servir de ligne d'attache, mais jamais de ligne de cote. Voir figure A
- Il faut éviter de répéter la même cote sur plusieurs vues, car on ne cote pas les vues mais la pièce
- La cote doit être portée par la vue ou le détail à coter apparaît le plus clairement.
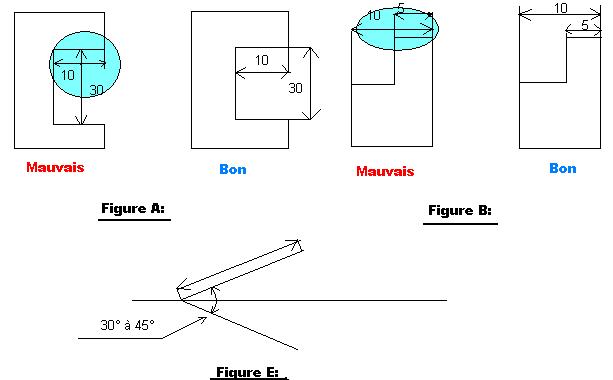
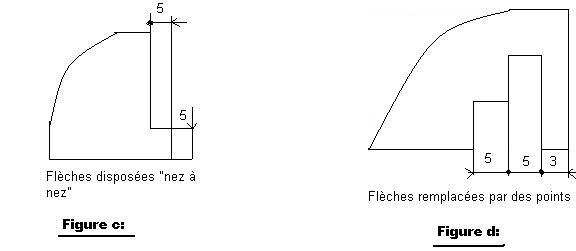
Les flèches se placent toujours aux extrémités de la ligne de cote. Les flèches sont faites au crayon donc demi tendre en trait fort leur angle d'ouverture varie entre 30° et 45° voir figure E.
On les placent normalement dos à dos mais peuvent être placées nez à nez si les segments à coter sont courts. Voir figure C. On peut les remplacer par les points alors si les segments son petits
Concours d'entrée aux grandes écoles
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale