Dynamique relativiste
Les bases de la relativité restreinte
Albert Einstein considéré comme le père de la dynamique relativiste, a émis deux postulats qui ne sont pas contradictoires avec la mécanique classique puis qu'il suffit simplement de redéfinir les grandeurs dynamiques:
- Les lois de mécanique ne changent pas lorsqu'on change de référence Galiléen, c'est-à-dire que la mécanique garde ses lois même formulation mathématique lorsqu'on passe d'un référentiel Galiléen à un autre.
- La vitesse de la lumière dans le vide est invariable quelque soit le référentiel Galiléen. Sa valeur c=3x108m/s n'est pas atteinte par des objets métalliques.
Expression de la quantité de mouvement et de l'énergie cinétique
Par définition le cœfficient:
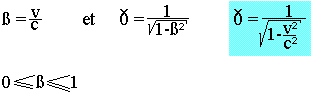
L'énergie totale d'un système de masse m est définie par la relation
l'électron volt
1ev = 1,6x10-19
1Mev = 106eV
Quantité de mouvement Mev/C
me = 9,1x10-31Kg
A partir d'une énergie de masse m animée d'une vitesse v on peut déterminer l'expression de son énergie cinétique
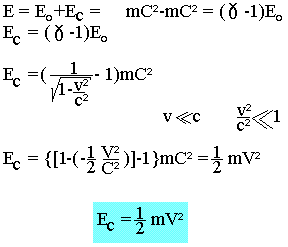
Une particule est donc considérée comme relativiste si sa vitesse
L'invariant relativiste
On montre que pour toute particule relativiste d'énergie totale E et de quantité de mouvement P.
E2 - P2C2 = E0
E2 - P2C2 = (mC2)2 = constante
Exercice 1:
Un électron se déplace à la vitesse de 10.000Km/s, calculer son énergie cinétique en Joule et en Mev (méga électronvolt).
Calculer la nouvelle valeur de son énergie cinétique si sa vitesse est de v=200.000Km/s
Exercice 2:
Une particule de masse m possède une énergie au repos de E0=1.785Mev et Ec=1.000Mev
Donnez sa quantité de mouvement en Mev/s et en Kgm/s puis en déduire sa vitesse.
Concours d'entrée aux grandes écoles
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale