Généralités
Pour résoudre le problème de retard de propagation des compteurs asynchrones, on utilise les compteurs synchrones. Dans les compteurs synchrones toutes les bascules sont déclenchées par l'horloge au même moment. Avant chaque impulsion d'horloge les entrées J et K des bascules JK (ou l'entrée D de la bascule D) doivent se trouver dans le niveau approprié pour assurer le passage de chaque bascule dans le bon état.
Exemple: Pour un compteur modulo 4 pour quitter de 1 à 2 les entrées des bascules JA KA et JB KB doivent se trouver au bon niveau logique pour que la sortie de la bascule A passe de 1 à 0 et la sortie de la bascule B passe de 0 à 1.
Compteur synchrone à bascule JK
Table de transition ou table d'excitation des bascules JK
Tables de vérité inversée de la bascule JK
|
Qn |
Qn+1 |
J |
K |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
||
|
0 |
1 |
1 |
0 |
|
1 |
1 |
||
|
1 |
0 |
0 |
1 |
|
1 |
1 |
||
|
1 |
1 |
0 |
0 |
|
1 |
0 |
Table de transition d'une bascule JK
|
Qn |
Qn+1 |
J |
K |
|
0 |
0 |
0 |
X |
|
0 |
1 |
1 |
X |
|
1 |
0 |
X |
1 |
|
1 |
1 |
X |
0 |
Compteur synchrone modulo 4 à bascules JK
Pour réaliser ce compteur il faut 2 bascules JK.
Table de transition du compteur
|
Etats |
QB |
QA |
JB |
KB |
JA |
KA |
|
0 |
0 |
0 |
0 |
X |
1 |
X |
|
1 |
0 |
1 |
1 |
X |
x |
1 |
|
2 |
1 |
0 |
X |
0 |
1 |
X |
|
3 |
1 |
1 |
X |
1 |
X |
1 |
|
0 |
0 |
0 |
0 |
X |
1 |
X |
On remplit les états de JK d'une ligne en considérant la sortie de cette ligne comme Qn et les sorties de la ligne suivante comme Qn+1
Exemple:
A l’état 0 (1ère ligne).
QB; Qn = 0 et Qn+1 = 0
QA: Qn = 0 et Qn+1 = 1
La dernière ligne est juste le report de la première.
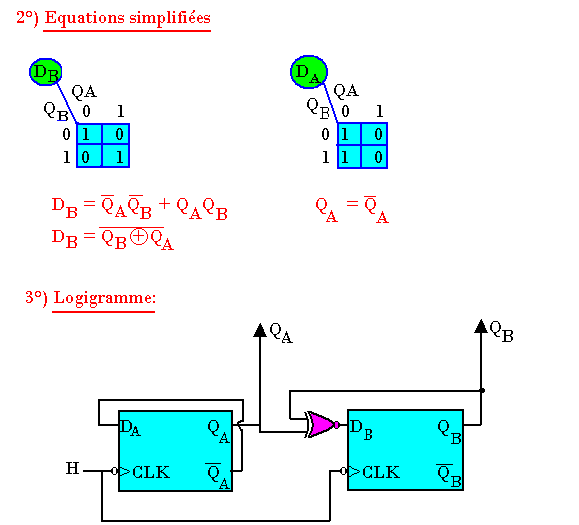
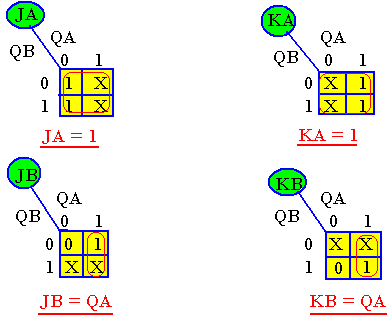
Simplification par tableau de Karnaugh
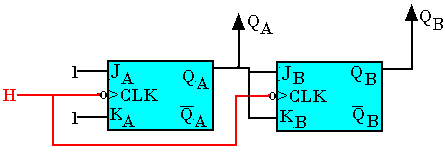
Logigramme
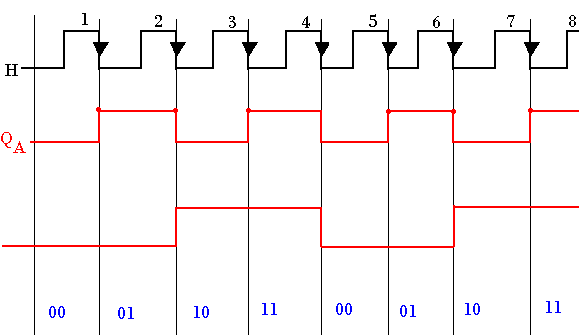
Chronogramme
Compteur synchrone à bascule D
Table de transition de la bascule D
|
Qn |
Qn+1 |
D |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Compteur synchrone modulo 4 à bascule D
Table de transition du compteur
|
Etats |
QB |
QA |
DB |
DA |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
2 |
1 |
0 |
1 |
1 |
|
3 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
Simplification par Karnaugh
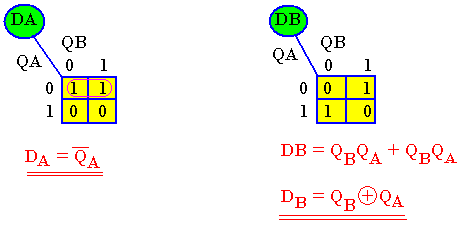
Logigramme
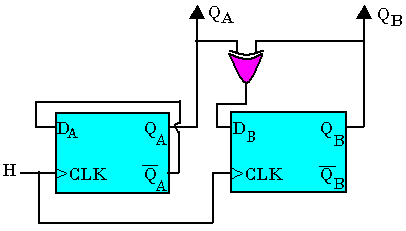
Chronogramme
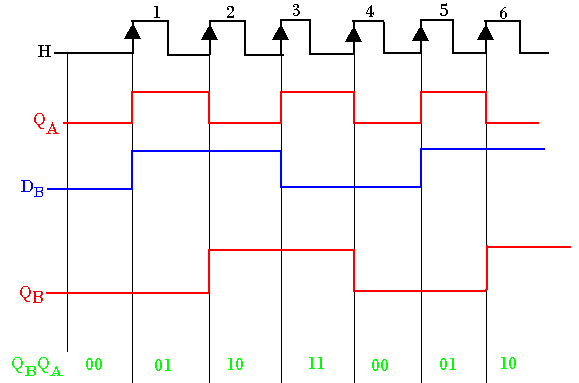
Compteurs synchrones modulo inférieur à 2n
Compteur synchrone modulo 7 à bascule JK
|
Etat |
QC |
QB |
QA |
JC |
KC |
JB |
KB |
JA |
KA |
|
0 |
0 |
0 |
0 |
0 |
X |
0 |
X |
1 |
X |
|
1 |
0 |
0 |
1 |
0 |
X |
1 |
X |
X |
1 |
|
2 |
0 |
0 |
1 |
0 |
X |
X |
0 |
1 |
X |
|
3 |
0 |
1 |
1 |
1 |
X |
X |
1 |
X |
1 |
|
4 |
1 |
0 |
0 |
X |
0 |
0 |
X |
1 |
X |
|
5 |
1 |
0 |
1 |
X |
0 |
1 |
X |
X |
1 |
|
6 |
1 |
1 |
1 |
X |
1 |
X |
1 |
0 |
X |
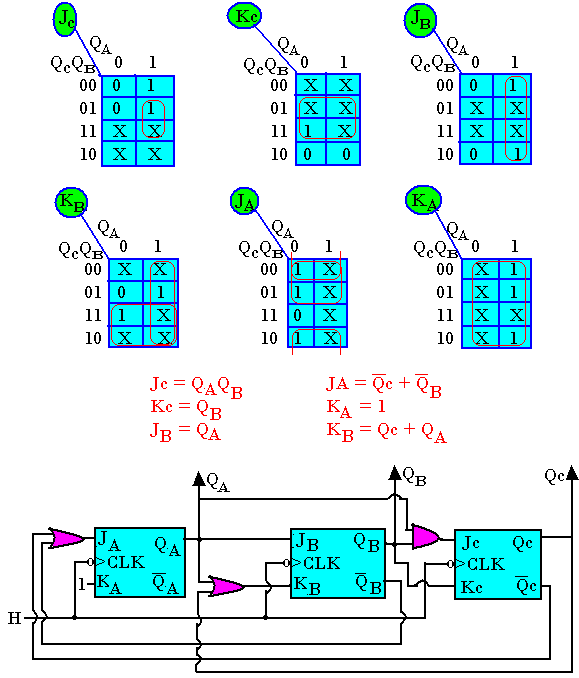
Compteur synchrone
Le principe de construction des décompteurs synchrones est le même que celui des compteurs synchrones. Il suffit d'établir la table de transition, sortir les équations et faire le logigramme à l'aide des bascules et portes logiques.
Exemple d'un décompteur synchrone modulo 4 à bascule D
1) Table de vérité:
|
Etats |
QB |
QA |
DB |
DA |
|
3 |
1 |
1 |
1 |
0 |
|
2 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
3 |
1 |
1 |
|
|