Généralités
En fonctionnement classe "A", il faut attendre que le transistor fonctionne tout le temps dans la région active. Le courant collecteur circule donc durant les 360° d'un cycle alternatif.
Amplificateur à couplage inductif
Les montages servant à amplifier la puissance doivent avoir une faible résistance collecteur. L'amplificateur à couplage inductif utilise une inductance L au collecteur. Cette inductance est choisie de telle sorte qu'elle se comporte comme un circuit ouvert pour les hautes fréquences et comme un court-circuit pour le continu.
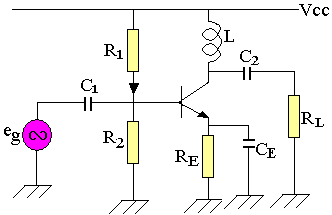
Soit rbb la résistance interne de la bobine, la résistance de charge statique est Rdc=RE+rbb=RE
L'équation de la droite de charge statique est VCC=RdcIC+VCE
En alternatif la résistance de l'alternatif est Rac=RL//(jLω) or Lω>>RL alors Rac=RL
Pour obtenir une dynamique maximale du signal de sortie, on choisit le point Q tel qu'il soit au milieu de la droite de charge dynamique, dans ce cas on peut écrire VCEQ=RacICQ
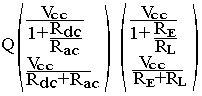
L'équation de la droite de charge dynamique dans ce cas est ic=-vce/Rac+b
L'équation passe par le point de repos.
VCC/(RE+RL) = -VCC/(RE+RL)+b ↔ b=2VCC/(RERL)
iC=-VCE/RL+2VCC/(RE+RL)
Si iC=0 VCE = 2VCC/(1+RE/RL) = 2VCC car RL est souvent supérieure à RE A(2VCC;0)
Si VCE=0 iC = 2VCC/(RE+RL) = 2ICQ B(0;2ICQ)
IC = -VCE/Rdc + VCC/Rdc
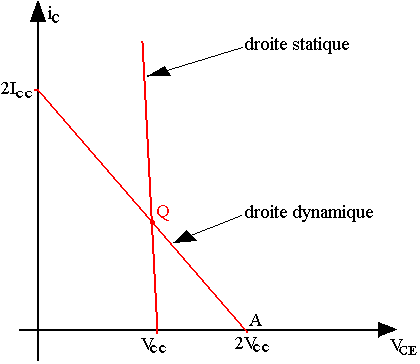
L'utilisation de l'inductance produit une excursion de la tension de sortie équivalente à un doublage de la tension d'alimentation.
Calcul des puissances
Puissance fournie par l'alimentation
PCC=VCC(ICQ+Ipont) or Ipont<<ICQ
PCC=VCCICQ=VCC.VCC/(RL+RE)=VCC2/(RL+RE)
or RE<<RL ; PCC=VCC2/RL
Puissance fournie à la charge
RL = V2Ceff/RL = V2Lmax/2RL or VL=VCE
VCmax = VCEmax = VCE
PL = VCC2/2RL
Le rendement du montage est : n = PL/PCC = 50%
La puissance maximale consommée par le transistor
Ptrans = VCEQ.ICEQ
Amplificateur par couplage amplificateur
Le transistor est souvent utilisé à la sortie d'un amplificateur pour permettre le maximum de transfert de puissance, car il permet de réaliser une adaptation d'impédance.
Adaptation d'impédance
La sortie d'un amplificateur peut être représentée par une source de tension V0 avec son impédance de sortie R0. On démontre que pour transférer le maximum de puissance à une charge RL; il faut RL=R0.
Ainsi on détermine qu'il y'a adaptation d'impédance pour adapter la charge à l'impédance de sortie d'un amplificateur, on fait appel à un transformateur.
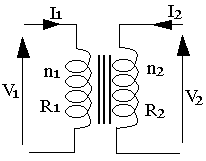
Soit R2 la résistance du secondaire, R1 la résistance du primaire, n1 le nombre de spire primaire, n2 le nombre de spire au secondaire, m est le rapport de transformation, V2 la tension secondaire, V1 la tension primaire.
Dans un transformateur parfait on a:
m = V2/V1 = n2/n1 = I1/I2
m2 = V2I1/V1I2 = R21/R1
m2 = R2/R1 = (n2/n1)2
R2 = n22R1/n21 ; R1 = R2n21/n22
R2 = m2R1 ; R1 = R2/m2
De ce qui précède une résistance de valeur fixe R2 est vue de primaire avec n'importe qu'elle valeur qui nous intéresse. Il suffit de trouver la valeur de m.
Exemple: Amplificateur de puissance à collecteur commun
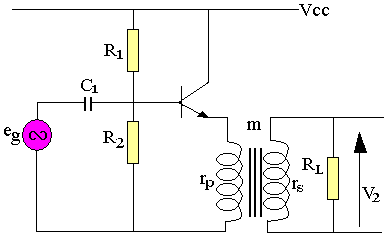
Droite de charge statique:
VCC = VCE+rpIC
IC = -VCE/rp+VCC/rp or rp tend vers 0
rp=RDC tend vers 0 et IC tend vers l'infini.
Droite de charge en alternatif:
iC = -vCE/Rac+b avec Rac=rp+RL/m2+rS/m2
Si on suppose que le point de repos Q est placé au milieu de la droite de charge dynamique, c'est-à-dire:
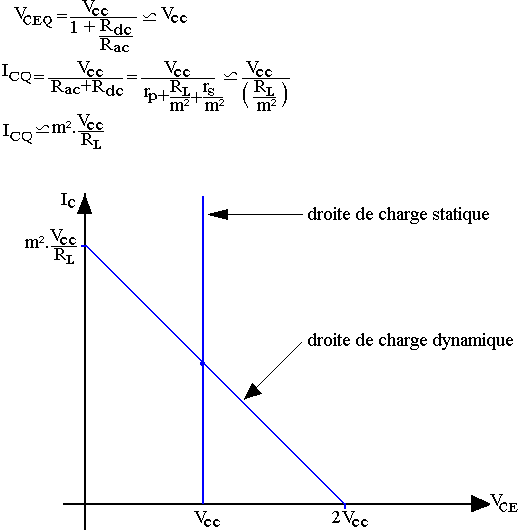
Calcul des puissances
- Puissance fournie par l'alimentation:
PCC=VCCICQ=VCCm2VCC/RL=mVCC2/RL - Puissance dans la charge:
PL=VLeff2/RL=VLeff2/2RL or VL/VCE=m ; VL=mVCE
VLmax=VCEmax=mVCC
PL=mVCC2/2Rl
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale