Moment du couple utile
Tem=KØI=K'I avec K'=KØ
Pe-Pu=Pc
Le moment du couple Tem=KØI s'écrit puisse que le couple est constant Tem=K'I, la relation entre I et T ne dépend pas de U
A cause des pertes magnétiques et mécaniques dont on appelle la somme Pc, la puissance utile Pu (sous forme mécanique) sous l'arbre du moteur est inférieur à la puissance magnétique Pe.
Pc = Pmag + Pméca
Tu=Pu/r < (pe/Pr=Te)
Te-Tu=TP=(Pe-Pu)/r=Pc/r=Kr/r=constante.
Le moment de couple de perte est constant.
Variation du couple utile avec le courant I
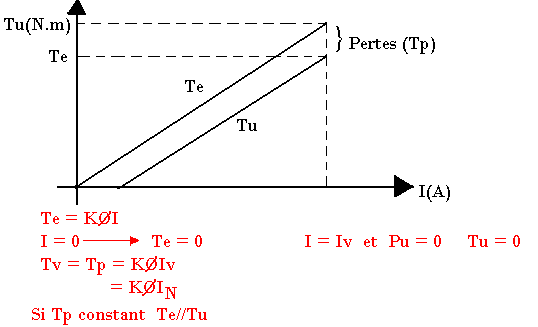
Caractéristique mécanique
La caractéristique donne les variations du moment de celle de la vitesse de rotation r. Cette courbe permet de choisir le moteur qui convient pour entraîner une charge donnée.
Tracé de la caractéristique
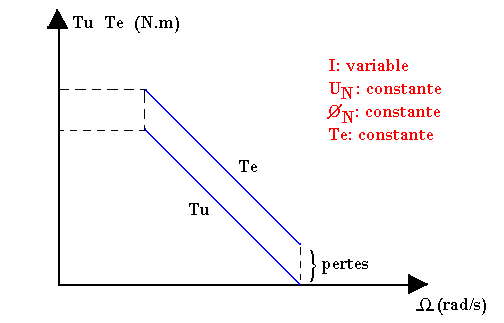
Pour un moteur à excitation indépendante, la courbe se trace à tension de l'alimentation et à flux constant. L'induit est alimenté en tension UN connaissant les variables de la vitesse r et celle Tu en fonction de l'intensité I. On trace point par point les variations TU en fonction de r. Avec Ø et U constant, r=rv-RI/KØ et Tu=KØI-TP.Tu est donc une fonction affine décroissante de r.
- orsque l'induit est alimenté sous tension constante, l'intensité du courant I et le moment du couple augmente et le couple utile Tu augmente avec la charge entraînée et la vitesse diminue.
- Lorsque la charge présente un couple de moment constant, le courant I reste constant si la vitesse varie.
- Le choix du mode de fonctionnement dépendra de la charge à entraîner.
Point de fonctionnement
La charge impose un couple résistant de moment Tr sur k'arbre qui tourne à la vitesse r. Le moteur doit fournir un couple utile TU=Tr en équilibre.
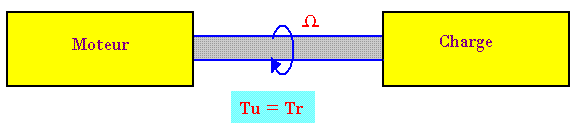
Le point de fonctionnement du groupe moteur charge entraîné se situe à l'intersection des caractéristiques mécaniques TU(r) et TR(r) des deux machines.
On utilise deux méthodes pour déterminer les coordonnées du point de fonctionnement
- Si l'on connaît les relations mathématiques TU(r) et TR(r), on résout l'équation Tu(r)=TR(r). S'il existe plusieurs solutions, on considère celle qui a un sens physique.
- Si l'on dispose des deux caractéristiques mécaniques du couple, on les trace sur la même feuille et on lit les coordonnées de leur point d'intersection.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale