Généralités
C'est un dispositif qui permet d'adapter le signal bande de base au canal de transmission. On rencontre plusieurs types de modulation: la modulation d'amplitude, la modulation de fréquence et la modulation de phase.
La modulation d'amplitude AM
Caractéristique de la modulation d'amplitude
- La modulation à bande latérale double (DSB)
- La modulation à bande latérale unique (SSB)
- La modulation à bande latérale résiduelle (VSB)
Supposons que nous disposons d'une onde modulante sinusoïdale fm(t)=AmCos(ωmt+þm) et d'une porteuse fc(t)=ACCos(ωCt+þC). L'onde modulé sera f(t)=[Ap+AmCosωmt]Cosωpt
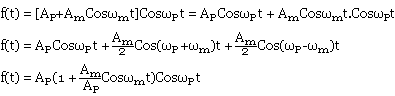
m=Am/Ap est l'indice de modulation.
f(t) = Ap(1+mCosωmt)Cosωp
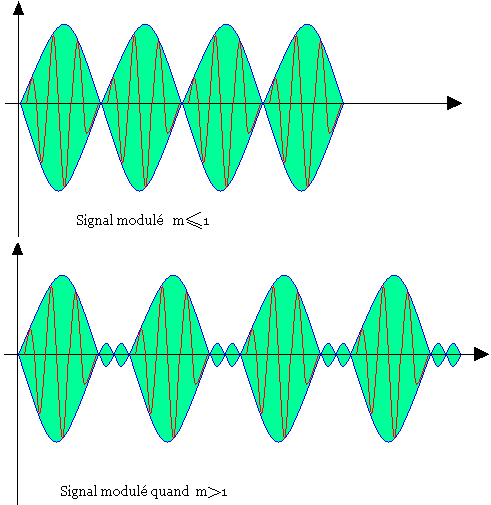
Pourcentage de modulation = m.100
Représentation spectrale d'un signal AM
Une onde AM se compose de 3 ondes: La porteuse Ap=Cosωpt et deux autres ondes de fréquence respective (ωp+ωm) et (ωp-ωm)
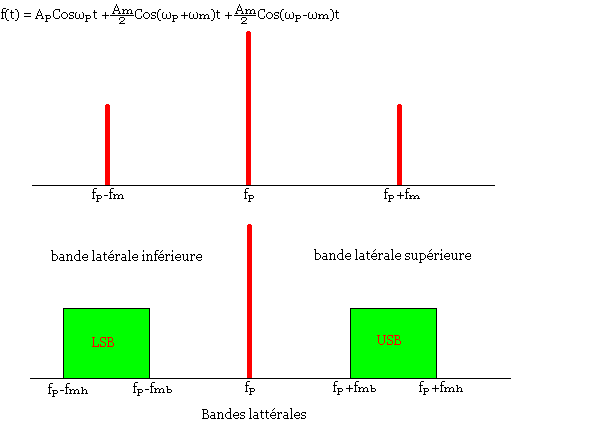
La bande latérale inférieure est toujours inverse du signal modulant.
La bande de fréquence d'un signal AM doit être 2fm ou fm représente la plus grande fréquence modulante.
LSB : Bande latérale inférieure.
USB : Bande latérale supérieure.
Relation de puissance
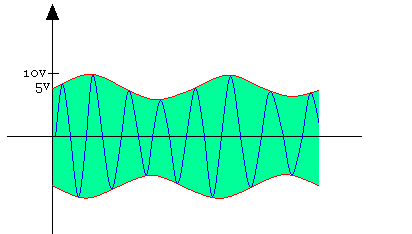
La figure représente un signal modulé en AM:
- Calculer l'indice de modulation
- Déterminer la modification à apporter à la porteuse pour avoir m=0,1 (indice de modulation)
Solution:
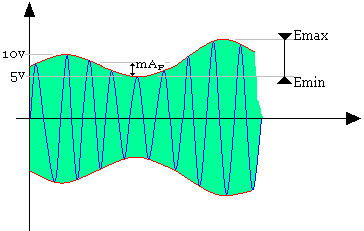
- Calculons m
m = Am/Ap = 5/10 = 0,5 - Pour que m=0,1 il faut que:
Emoy = (Emax+Emin)/2 = (10+5)/2
Emoy = 7,5V
m = (Emax-Emin)/(Emax+Emin)
m = (10-7,5)/17,5 = 0,14
Relation de puissance
![]()
La puissance moyenne d'une onde AM, PT peut être exprimée en fonction de la puissance moyenne porteuse Pp et la puissance moyenne des bandes latérales PLSB et PUSB.
Si une onde AM est émise via une antenne de résistance E, les puissances moyennes seront proportionnelles au carré des valeurs efficaces. On aura:
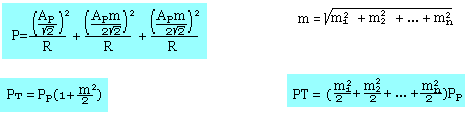
Si l'indice de modulation m=1, nous remarquons que la puissance contenue dans les bandes latérales ne peut excéder 1/6 de la puissance émise. La porteuse du signal AM contient donc au moins 2/3 de la puissance totale émise.
On appelle cette modulation, la modulation double bande latérale DSB.
En modulation à double bande latérale, la porteuse qui ne porte pas l'information absorbe les 2/3 de la puissance émise par l'émetteur. Pour améliorer la modulation, on utilise la modulation à double bande latérale avec suppression de la porteuse.
La SSB a l'avantage qu'il porte deux fois plus d'information étant donné que la bande de fréquence d'un signal SSB est égale à la moitié de bande de fréquence d'un signal AM ou DSB.
Exercice:
Une fréquence modulante de 250 Hz est modulée par une fréquence de 400Hz.
Quelles sont les fréquences de la bande latérale?
La fréquence de la bande latérale:
400 - 250 = 150Hz
Rendement de la puissance AM
Le rendement est égale à la puissance de la bande latérale sur la puissance totale de la porteuse: n=PUSB/PT
Détection d'enveloppement du signal AM
Détection hétérodyne
L'hétérodyne est un processus qui mélange deux fréquences pour obtenir une autre. La modulation d'amplitude est un processus hétérodyne. Le signal de l'information est misé avec celle de la porteuse pour produire des bandes latérales.
Détection superhétérodyne
Superhétérodyne est le processus où les mélanges des deux fréquences donne une fréquence inférieure à celle d'origine.
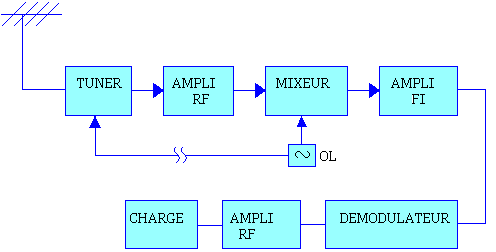
Au niveau de l'antenne, on a une multitude de fréquence à capter, mais l'on aura besoin d'un seul signal utile pour la charge, c'est donc en faisant varier la fréquence générée par l'oscillateur local manuel qui va attaquer le tuner, ensuite le tuner sélectionnera une fréquence de notre choix à travers l'antenne. Le tuner ayant sélectionné une fréquence, ce signal sera très faible de l'ordre des µV. Le signal étant très faible, il sera amplifié par l'Ampli RF. Le signal amplifié attaquera ensuite le mixeur, qui mixera ce signal avec la fréquence de l'oscillateur local (OL). A la sortie du mixeur, on a donc le signal sélectionné modulé en AM, qui sera ensuite amplifié par l'ampli FI et ensuite subira une démodulation AM à travers le démodulateur pour avoir le signal modulant qui sera ensuite amplifié par l'ampli BF puis à sa sortie alimentera la charge.
Les modulations en fréquence
En modulation en fréquence, l'information est portée par une modulation de la fréquence de la porteuse et non par une variation d'amplitude.
Caractéristique de la modulation de fréquence
La fréquence de la porteuse devra varier linéairement en fonction de l'information modulante fm(t).
Soit une onde sinusoïdale fp(t)=ApCosωpt appelée onde porteuse
La fréquence instantanée sera: fp+Kffm(t).
La pulsation d'une onde sinusoïdale n'est rien d'autre qu'une vitesse angulaire, c'est donc la dérivée de l'angle de phase.

La pulsation ou vitesse angulaire ωp représente ici le taux de variation de l'angle par rapport au temps. De même la puissance angulaire instantanée ω(t) d'une onde modulée en fréquence est défini comme le taux de variation de l'angle de phase.
En supposant un message modulant du type
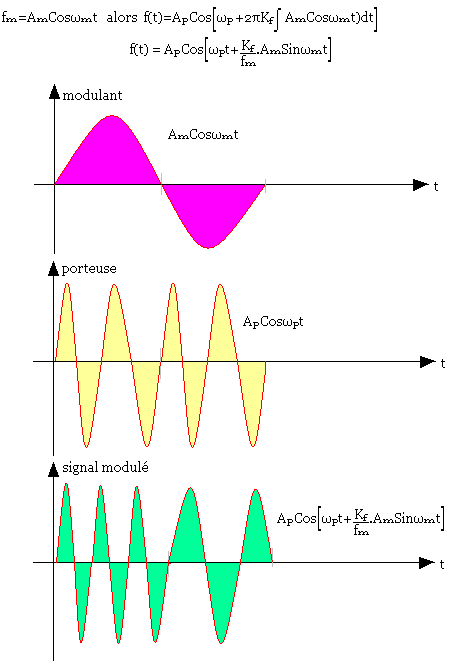
Lorsque le message modulant est sinusoïdal, la fréquence de l'onde modulée est fp+KfAmCosωmt. Celle-ci varie entre fp-KfAm et fp+KfAm, la déviation maximale de fréquence est donc KfAm et est appelée excursion de fréquence.
fp : fréquence de la porteuse.
fm : fréquence du signal modulant.
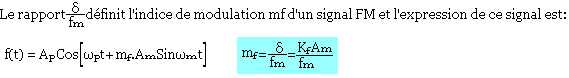
Spectre d'un signal FM
Un signal FM donc la porteuse et le message modulant ont des fréquences angulaires respectives ωp et ωm, possède un nombre infini de composant spectral situé à ωp±nωm, n est un nombre entier (0;1;2...).
L'amplitude correspondante à ces fréquences est déterminée par des cœfficients Jn(mf) connu comme fonction de Bessel.
f(t) = ApCos[ωpt+mfSinωmt] = ApCosωptCos(mfωmt-ApSinωptSin(mfSinωmt).
Un signal modulé en fréquence peut s'exprimer en forme exponentielle en écrivant de la façon suivante:
![]()
Un signal en modulation en fréquence se compose donc d'une porteuse non modulée accompagnée de plusieurs composants modulés en amplitude.
Son spectre de Fourrier comporte donc une porteuse non modulée accompagnée des spectres centrée sur ωp.
Il est donc clair qu'il y'a pas de relation simple entre le spectre de Fourrier d'un signal en modulation de fréquence et le spectre du signal modulant la porte comme dans le cas de AM.
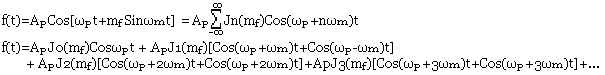
La variation des fonctions de Bessel en fonction de l'indice de modulation est représentée dans un tableau. Ces fonctions sont les solutions de l'équation m2d2f/d2mf+mfdf/dmf+(m2f-n2)f=0
Les variations de Bessel peuvent être calculée à partir de l'expression:
![]()
En pratique on utilise des tables où seront représentées les fonctions de Bessel dont l'amplitude est supérieure ou égale à 0,01. La raison du choix de cette valeur est qu'en fait les composants spectraux de très faibles amplitudes peuvent être négligées sans pourtant affecter l'allure du signal FM.
Propriété du spectre d'un signal FM
- Un signal a un nombre infini de composants spectrales distantes de fm, 2fm, 3fm de la fréquence de la porteuse, ces composantes sont séparé de par une distance fm sur l'axe des fréquences.
- Les raies spectrales pour lesquelles l'amplitude de cœfficient de Bessel est supérieure à 0,01 ne diminuent pas nécessairement leur amplitude lorsque n augmente; quoique dépasser une certaine valeur de n toutes les raies spectrales sont d'amplitude négligeable. Il en suit que la bande de fréquence FM dépend de l'indice de modulation mf et de la fréquence modulante fm
- e spectre présente une symétrie par rapport à la porteuse.
- Un indice de modulation plus importante implique une bande de fréquence plus grande.
- En AM, l'augmentation de l'indice de modulation est suivie d'une grande puissance de la bande de fréquence alors qu'en FM, la puissance totale du message reste constante quelque soit le message.
- Notons que le cœfficient de Bessel J0(mf) correspond à fréquence de la porteuse et varie selon l'indice de modulation.
- Pour une même excursion de fréquence, une fréquence modulante plus élevée se traduit par n nombre moins important de raies spectral diminue.
- La bande de fréquence du signal FM dépend de l'indice de modulation ainsi que de la fréquence modulante
- Si mf<<1, le spectre d'un signal FM rappel celui d'un signal AM et nous obtenons une modulation en bande étroite NBEF (Narrow Band FM). La bande de fréquence Bfm du signal est Bfm=2fm
- Si mf appartient à l'intervalle [0,3;20] la bande de fréquence sera déterminée à partir du nombre n de raies spectral dont l'amplitude du coefficient de Bessel demeure 0,01. On aura Bfm=2nfm
- Si mf>20 nous utiliserons la formule Bf=2[1+mf]fm
