Généralités
Forme algébrique d'un nombre complexe
L'ensemble des nombres est noté C.
C est aussi un espace vectoriel à deux dimensions: base (e1=1; e2=i)
Opération algébrique dans C
Soit z1 et z2 dans C, z1=a1+ib1 et z2=a2+ib2 alors on a les relations:
- Egalité: z1=z2
Re (z1)=Re (z2)
Im(z1)=Im(z2) - Sommation: z1±z2=(a1±ib1)±(a2+ib2)=(a1±a2)+(bn1±b2)
Re(z1+z2)=Re(z1)+Re(z2)
Im(z1+z2)=Im(z1)+Im(z2)
Module de Z:
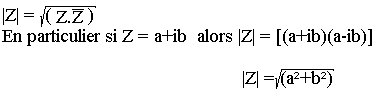
Autres relations remarquables
Si Z=a+bi
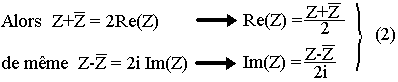
Forme trigonométrique d'un complexe
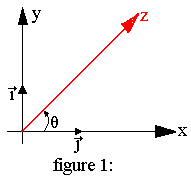
Soit donnée la représentation d'un complexe z dans le plan C:
- Le module de z est la distance OM
- L'argument de z (noté Arg(Z)) est la détermination principale de l'angle (OX,OM)
Ainsi on établit pour z plusieurs notations simplifiées.
Fonctions à variable complexe
Soit f une fonction définie de C→C
Limite et continuité
- La fonction f admet une limite L en Z0 si
- f test continue en Z0 si
lim f(Z) = f(Z0)
Z → Z0
Dérivée, différentielle d'une fonction complexe
On appelle dérivée de la fonction complexe ƒ(Z) le rapport
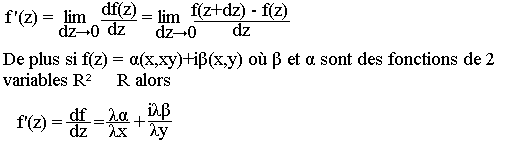
Différentiel d'une fonction complexe
Une fonction f: z → f(z) est différentiable en z0 si
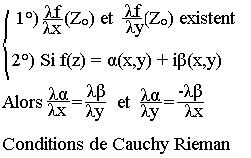
Exercice 1:
Soit ƒ(z)=ez-2iz
ƒ est-elle différentiable dans C
Exercice 2:
Dérivées des fonctions usuelles dans C
Z appartient à C
(zn)' = nZn-1
(ez)' = ez
(cosZ)' = -Sin
(SinZ)' = CosZ
(linZ)' = 1/Z
(Arc SinZ)' = 1/(1-Z2)½
(Arc CosZ)' = -1/(1-Z2)½
(Arc tgZ)' = 1/(1+Z2)
(ShZ)' = ChZ
(ChZ)' = ShZ
Fonction analytique
Si f est continue sur un domaine D et dérivable partout sur D, on dit que f est analytique sur D.
m connexité
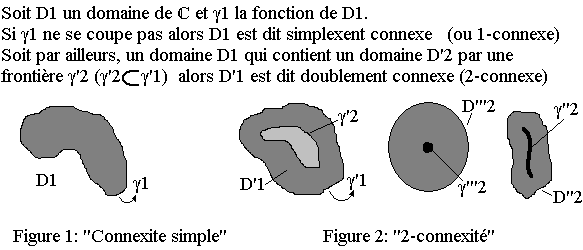
On définit de la même manière des domaine: 3-connexes; 4-connexes; ...; m-connexes.
Une frontière interne peut être réduite à un point, on a un segment.
Représentation conforme
Soit Z=x+iy et f(z) = x'+iy' une fonction analytique sur D. Soit A(x0,y0) appartenant à D, alors la représentation conforme du point A par f est le point f(A) d'affixe n0x'+iµ0y' dans le repère (o,x',iy').
La transformation conforme consiste en passage du repère (o, x, iy) vers (o,f(x),f(iy)).
Exercice:
Soit f(z)=Z3.
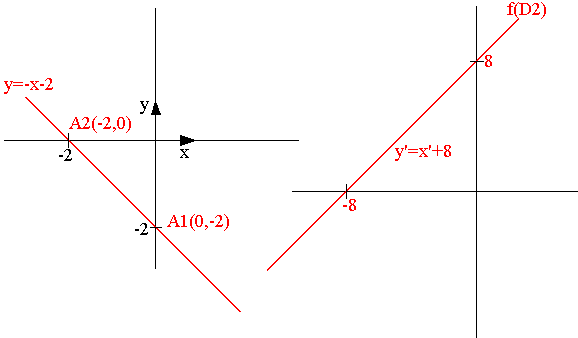
Déterminez la transformation conforme des droites D1 et D2 d'équation respectives: y=x et y=-x-2
Correction:
Posons Z=x+iy → f(z)=-Z3=x'+iy'
Z3=(x+iy)3=x3-3xy2+[-y3+3x2(y)] (E)
Pour trouver l'image de (D1) on introduit y=x dans (Z)
x = y
x' = x3 - 3x(x)2 = -2x3
y' = -(x)3 + 3x2(x) = 2x3
x' = -y', c'est l'image de D
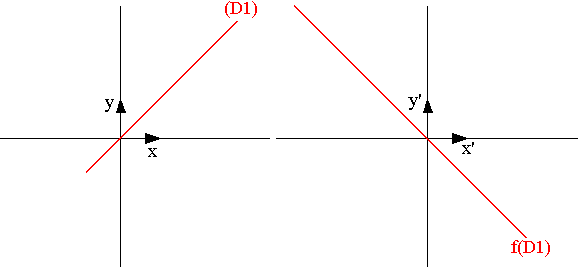
Pour trouver l'image de D2, on remplace y=-x-2 dans (E). Ou bien (2), déterminons les transformées de deux points de D2
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale