Fonction primitive
Soit f une fonction continue sur un intervalle [a, b].
On appelle primitive de f sur [a, b] une fonction F(ƒ) telle que dF(ƒ)(x)/dx=ƒ(x)
Propriété:
Soit f continue sur [a, b], alors deux primitives de f notées F1 et F2 sont telles que F1(x) et F2(x) = constante quelque soit x appartenant à [a,b]. Géométriquement, si y=F1(x) et Z=F2(x) sont deux primitives de f sur [a, b] de courbes respective C'1 te C2 alors les tangentes en x0 à C1 et à C2 sont parallèles.
Corollaire
Si ƒ est continue sur [a, b] alors f admet une infinité de primitive sur [a, b].
Notion d'intégrale définit
Soit f une fonction sur [a, b] et F une primitive de f sur [a, b], alors l'intégrale définie de ƒ(x) sur [a, b] est le réel
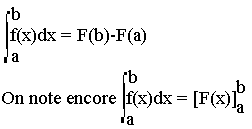
Propriétés
On suppose f continue sur [a, b]

Limite d'une somme de Riemann
Approximation de Riemann
Soit f une fonction continue sur un intervalle [a, b] et Cƒ sa courbe représentative sur un R.O.N (x, o, y). Nous nous proposons de calculer l'aire du trapèze curviligne limité par Cƒ, l'axe ox et deux parallèles (D1) et (D2) d'équation respectives x=a et a=b
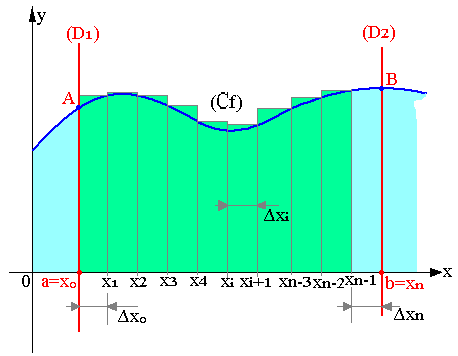
Si A est l'aire du trapèze curviligne aABb on peut approcher la valeur de S, somme des n boucles subdivisent aABb. Chaque baud verticale est considérée comme rectangle élémentaire de base xi+1-xi et de hauteur ƒ(xi).
Chaque bande élémentaire a donc une surface élémentaire. La surface de la ligne en escalier

Théorème de la moyenne
Théorème
Si f est contenue dans un intervalle [a, b], alors:
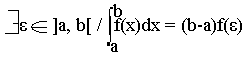
Exercice:
- Démontrez le théorème de la moyenne à l'aide du théorème des accroissements finis.
- L'intensité d'un courant alternatif a pour expression I=ImaxSin360t/T. Calculez la valeur moyenne de carré de l'intensité du courant pendant la période T. Calculez ainsi ma valeur efficace du courant I.
