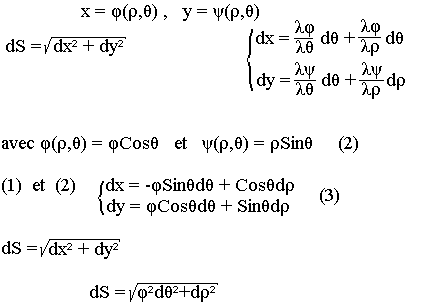Fonction primitive
Soit f une fonction continue sur un intervalle [a, b].
On appelle primitive de f sur [a, b] une fonction F(ƒ) telle que dF(ƒ)(x)/dx=ƒ(x)
Propriété:
Soit f continue sur [a, b], alors deux primitives de f notées F1 et F2 sont telles que F1(x) et F2(x) = constante quelque soit x appartenant à [a,b]. Géométriquement, si y=F1(x) et Z=F2(x) sont deux primitives de f sur [a, b] de courbes respective C'1 te C2 alors les tangentes en x0 à C1 et à C2 sont parallèles.
Corollaire
Si ƒ est continue sur [a, b] alors f admet une infinité de primitive sur [a, b].
Notion d'intégrale définit
Soit f une fonction sur [a, b] et F une primitive de f sur [a, b], alors l'intégrale définie de ƒ(x) sur [a, b] est le réel
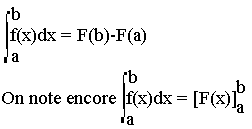
Propriétés
On suppose f continue sur [a, b]

Limite d'une somme de Riemann
Approximation de Riemann
Soit f une fonction continue sur un intervalle [a, b] et Cƒ sa courbe représentative sur un R.O.N (x, o, y). Nous nous proposons de calculer l'aire du trapèze curviligne limité par Cƒ, l'axe ox et deux parallèles (D1) et (D2) d'équation respectives x=a et a=b
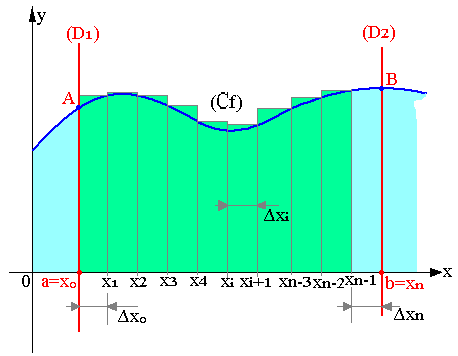
Si A est l'aire du trapèze curviligne aABb on peut approcher la valeur de S, somme des n boucles subdivisent aABb. Chaque baud verticale est considérée comme rectangle élémentaire de base xi+1-xi et de hauteur ƒ(xi).
Chaque bande élémentaire a donc une surface élémentaire. La surface de la ligne en escalier

Théorème de la moyenne
Théorème
Si f est contenue dans un intervalle [a, b], alors:
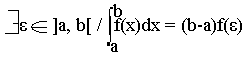
Exercice:
- Démontrez le théorème de la moyenne à l'aide du théorème des accroissements finis.
- L'intensité d'un courant alternatif a pour expression I=ImaxSin360t/T. Calculez la valeur moyenne de carré de l'intensité du courant pendant la période T. Calculez ainsi ma valeur efficace du courant I.
Intégrales impropres
Intégrales à supports non bornés

ii) Par extension de i) si g est continue sur R
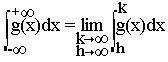
Conséquences
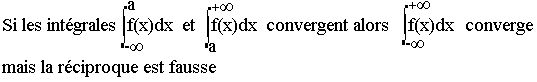
Intégrale à support ouvert et bornée
Soit f une fonction continue sur un support ouvert et bornée du type ]a,k[ ou ]a,k[ ou [a,k[ alors:
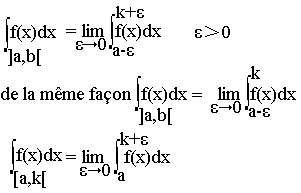
Intégrales en coordonnées polaires
Passage des coordonnées rectangulaires aux coordonnées polaires
Caractérisation
Un pont M(x0, y0) du plan xoy est entièrement caractérisé par son module et son argument.
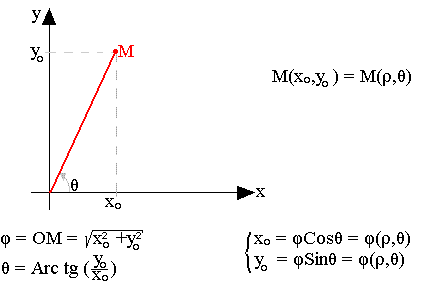
x0, y0 sont des fonctions de deux variables indépendantes.
Caractérisation de la longueur d'un arc du plan
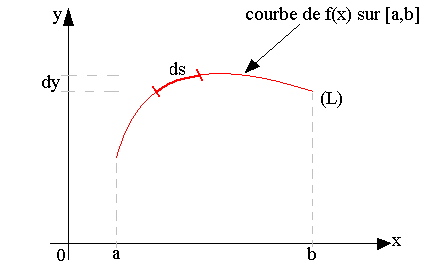
ds un élément de la portion de courbe C.
On a ds (différentielle de l'arc C)

Longueur d'une courbe en coordonnées polaires
On a pu montrer que