Les principaux théorèmes
Nombres premiers
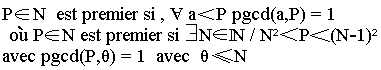
- Deux nombres entiers a et b sont premiers entre eux si PGCD (a, b)=1
Petit théorème de Fermat
![]()
Indicatrice d'Euler "Ø"
Déterminez le nombre d'entier ki/ki<P et PGCD (ki, P)=1
Exemple:
Ø(17)=16 ; Ø(12)=4
- Si p est premier Ø(p)
- Si p est premier Ø(pk)=pk-1(p-1)
- Si p et q sont premiers: Ø(p.q)=(p-1)(q-1) et Ø(pa.qb)=Ø(pa).(qb)
Théorème de Gauss
Si a>0 et p est premier (avec PGCD(a,b)=1) alors ac(p)=1[p]
Identité de Bézout
Si PGCD(a,b)=1 alors il existe M, M appartenant à Z* tel que Ma+Nb=1 ; (Ma=1[b] ou Nb=1[a])
Corps Z/PZ
Si p est premier alors (Z/PZ,+,x) est un corps commutatif.. En particulier tout élément admet un inverse.
Résidus quadratiques
a est un "résidus quadratique modulo p" si:
![]()
Exemple:
Montrez que X2=2[3] n'a pas de solution ("2" est-il résidu quadratique de Z/3Z)
Z/3Z = {0, 1, 2} = {0, 1, -1}
02 = 0[3]
12 = 1[3]
22 = 1[3]
X2 = 2[3] n'a pas de solution.
Théorème des restes Chinois
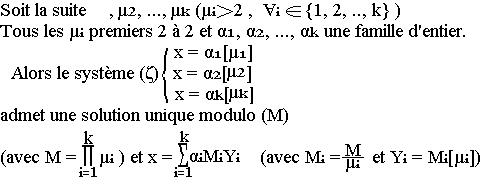
Grand théorème de Fermat
Si N est supérieur ou égal à 3, il b'existe pas (x, y, z) appartenant à Z/ xN+yN=zN
Nombre de diviseur d'un entier N
Si N=P1k1.P2k2....P5k5 où les Pi sont premier, alors le nombre de division de N et D(N)=(1+k1)(1+k2)...(1+k5)
Exemple:
Déterminez le nombre de diviseur de (391), (72), (101)
-394 = 171x231 ↔ D(391)=(1+(1))(1+(1))=4
Liste {1, 17, 23, 391}
Nombres premiers
On montre qu'il existe une infinité de nombre premier, l'ordre de succession des nombres premiers n'obéit à aucun reste commun, cependant on peut "cibler" des familles infinies de nombres premier à partir de certaines équations. C'est le cas par exemple des nombres de Mersenne et des nombres de Fermat.
Nombres premiers de Mersenne et de Fermat
Nombre de Mersenne
Ce sont les nombres de la forme NMe(P)=2P-1 avec P premier.
Exemple:
P=2 ; NMe(2)=3
P=3 ; NMe(3)=7
P=5 ; NMe(5)=31
P=7 ; NMe(7)=127
P=17 ; NMe(17)=131071
Nombres de Fermat
Ce sont des nombres de la forme NFe(N)=(22N+1-1)/(22N-1) avec n appartenant à N.
Recherche de nombres premiers
L'identification de Bézout nous rappelle que si deux nombres a et b sont premier entre eux,n il existe deux entiers relatifs M et N tels que aM+bM=1 (E)
L'algorithme d'Euclide nous permet de calculer M et N en faisant des divisions successives.
Exemple:
Supposons a<b, effectuons la division de b par a b=aq+r=aq1+r1, effectuons la division de a par 1 (car a>r1)
Exercice:
2632 et 29 sont premier entre eux, trouvons M et N tel que 2632(M)+29(N)=1
2632 = 90.29+22
29 = 1.22+7
22 = 3.7+1
1 = (2632-90.29) - [29-22]
1 = (2632-90.29) - 3[29-(2632-90.29)]
1 = 2632(1+3)+29(-90-30-270)
1 = 2632(4) + 29(-363)
Même question pour:
a = 1631 et b = 64
a = 3250 et b = 103
