Généralités

Etudions le cas de deux variables.
On considère la fonction f:(x,y) → f(x,y).
f admet un maximum au point P(a, b) lorsque pour tout point M(x, y); f(x, y) est inférieure ou égale à f(a, b)

Condition nécessaire d'extrémum

Il est nécessaire que:

On obtient les points critiques.

Condition suffisante

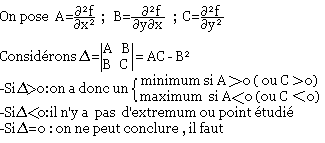
faire une étude approfondie utilisant le développement de Taylor à plusieurs variables. 

Situation où il y'a une contrainte sur les variables

On peut étudier les extrema de f sur une région du plan soumise à la contrainte φ(x,y)=0.
Dans ce cas on forme l'équation de Lagrange:

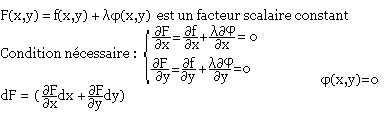
Pour les conditions suffisantes

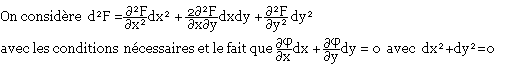
Si d²F < 0, alors on a un maximum.
Si d²F > 0, alors on a un minimum.

On pourrait aussi poser:

Si A₁C₁-B₁²>0 alors on aura:

De façon analogue on pourrait étudier le cas de trois variables, celui-ci requiert des calculs plus délicats dans le cas de contraintes sur les variables.

Exemple 1:

f(x, y) = x³+3xy²-15x-12y

Exemple 2:

f(x, y) = 6-4x-3y avec M(x, y) appartenant au cercle trigonométrique.

Cas d'extrema sur un domaine fermé borné connexe de R² et convexe

(D) = domaine fermé borné connexe de R² et convexe.
Si f est de classe C¹ sur (D) alors f est bornée sur (D) et atteint ses bornes au bord de (D).

Exemple:

f(x, y) = x²+y²-xy+x+y sur le domaine

Formule de Taylor

Nous allons donner la formule pour le cas d'une fonction à 3 variables.
f est une fonction scalaire de variable x, y, z.

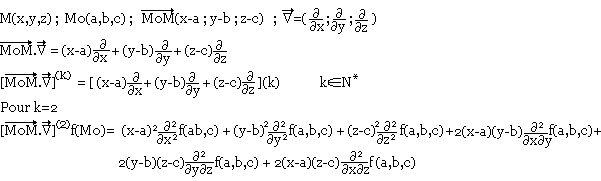
La formule de Taylor est donc:

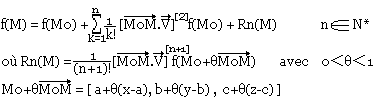
Posons (a, b, c) = (0, 0, 0) ; M₀ = O(0, 0, 0)
h=MM₀=(x, y, z), on aura alors la formule de Taylor Maclaurin.

Exemple 1:

Ecrire la formule de Taylor Maclaurin d'ordre 2 pour f(x, y)=-2e^xSiny

Exemple 2:

Ecrire la formule de Taylor Maclaurin d'ordre 2 pour g(x, y, z)=x³-2xyz²-4x²yz+7x

Exemple 3:

Ecrire la formule de Taylor au voisinage du point A(1;-1) d'ordre 2 pour h(x, y)=2x²Cosx+e^-xy