La cinématique est l'étude des mouvements des corps sans la prise en considération des causes qui les produisent. Un mouvement est une variation par rapport au temps de la position dans l'espace d'un solide. Le mouvement d'un système ne se définitif que par rapport à un point ou solide de référence appelé référentiel. L'objectif en mouvement est mobile.

Cinématique du point

Pour déterminer à chaque instant la position d'un mobile on convient de choisir une origine liée à un repère d'espace et un instant ou une date initiale liée à un repère de temps.

Le vecteur position

Dans le repère (o, i, j, k) la position d'un point M à un instant t est déterminée par le vecteur OM=xi+yj+zk appelé vecteur position x, y et z coordonnées du point M sont fonction du temps.

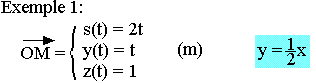
Ceci est appelé équation paramétrique ou encore équation horaire.
En éliminant t dans les équations horaires, on obtient une relation qui traduit l'ensemble des positions successivement occupées par le mobile pendant sont déplacement: On l'appelle la trajectoire
Le mouvement est dit rectiligne si sa trajectoire est une droite curviligne, si elle est circulaire, elliptique, parabolique... L'unité des coordonnées d'espace x(t), y(t), z(t) est le mètre, l'unité de temps est la seconde.

Le vecteur vitesse

On montre que les coordonnées du vecteur vitesse instantané sont obtenues en dérivant celles du vecteur position

Le vecteur vitesse renseigne sur la vitesse à chaque instant t du mobile. Son module v est exprimé en m/s
v = (x²+y²+z²)^½

Le vecteur accélération

L'accélération instantanée caractérise les variations du vecteur vitesse. Les coordonnées du vecteur accélération sont obtenues par dérivation du vecteur vitesse.

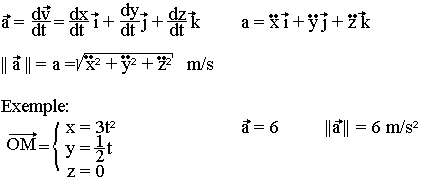
Le mouvement est uniformément varié

Le vecteur accélération peut être décomposé en deux vecteurs orthogonaux a_n et a_t appelée accélération normale et accélération tangentielle. Les vecteurs a_n et a_t sont portés par deux vecteurs unitaires orthogonaux n et t, d'un repère de Fresnel.

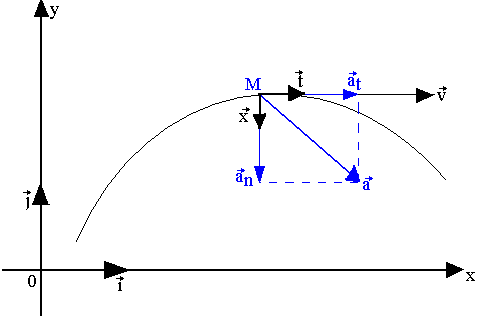
Le vecteur t est tangent à la trajectoire au point M et le vecteur n lui est normal au même point.

Remarque:

• Si la trajectoire est une droite a_n=0 donc a=a_t
• Si la trajectoire est un cercle, le rayon de courbure Þ=R