Miroirs plans
On appelle miroir plan toute surface plane réfléchissante.
Stigmate du miroir plan
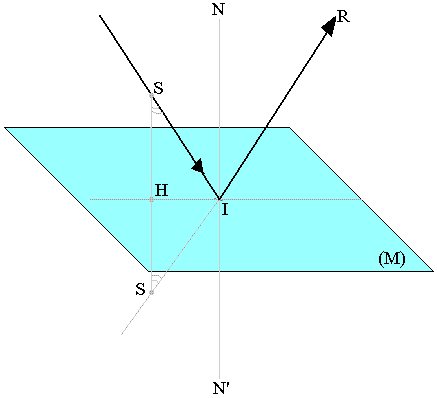
Considérons le miroir M et un objet lumineux (S). Le rayon SH perpendiculaire à M a pour rayon réfléchi le rayon HS. L'image S' de S si elle existe appartient à la droite SH. Un autre rayon incident SI se réfléchit suivant IR tel que SÎN=NÎR or SH//NI ce qui veut dire que l'angle HSI égal l'angle IS'A. Le triangle ISS' est isocèle et S' est le symétrie de S par rapport au plan du miroir.
Enoncé:
Le miroir plan est le seul système optique rigoureusement stigmatique.
Dioptre plan
Un dioptre plan est un système optique constitué par deux milieux optique transparent séparés par une surface plane.
Image d'un point – stigmatisme
L'objet (S) est à l'infini
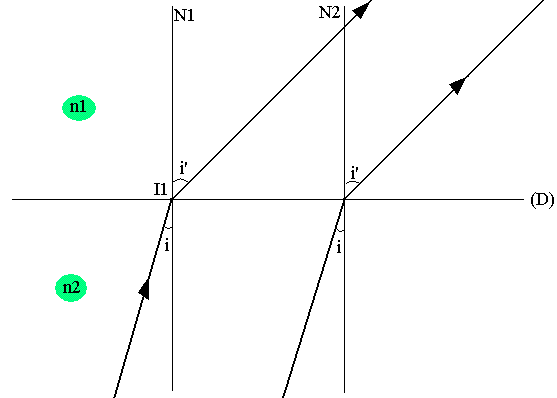
(S) est à l'infini, ce qui signifie que le rayon arrivant sur le dioptre est cylindrique par conséquent le faisceau émergeant est aussi cylindrique. Donc S' est à l'infini.
S étant à l'infinie et S' étant à l'infini on dit qu'il y'a stigmatisme rigoureux.
L'objet (S) est à une distance finie
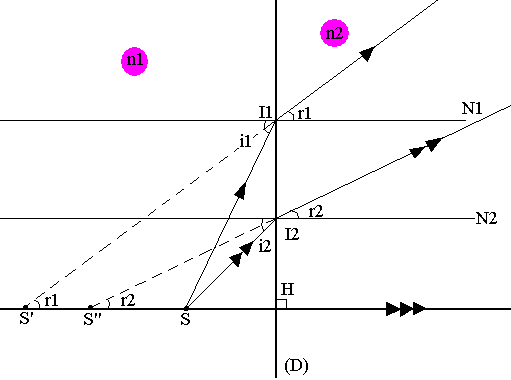
Considérons un point objet lumineux (S) dans le milieu d'indice n1. Le rayon normal au dioptre SH traverse (D) sans être dévié. Toute image de (S) si elle reste appartient à la droite (SH). Par ailleurs le rayon incident SI1 travers le dioptre avec un angle de réfraction r1 avec n1Sin(i1)=n2Sin(r1). Le rayon réfracté de SI1 semble provenir de S'. On peut alors écrire que:
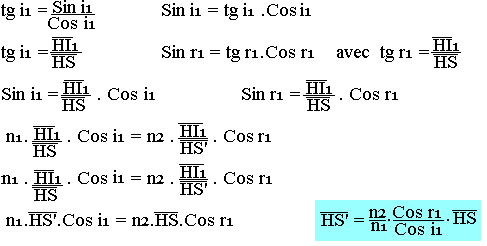
Quand I1 varie le rapport Cos(r1)/Cos(i1) varie aussi, ainsi pour un objet donné (S), (S') n'est pas fixe. On dit qu'il y'a pas stigmatisme.
Enoncé:
Pour un dioptre plan il y'a pas de stigmatisme rigoureux dans le cas d'un point objet situé à une distance finie.
Stigmatisme approché
Si on considère des rayons peut inclinés par rapport à la normale et voisin de cette normale.
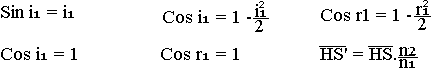
- Si n2>n1, le milieu d'indice n2 est plus réfringent que le milieu d'indice n1 ; HS'>HS. L'image s'éloigne de la surface de séparation.
- Si n2<n1; HS'<HS; l'image se rapproche de la surface de séparation.
