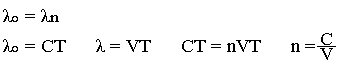Page 1 sur 4
Généralités
La lumière se manifeste généralement sur deux aspects: l'aspect corpusculaire et l'aspect ondulatoire.
Aspect corpusculaire
Dans les échanges d'énergie avec la matière, la lumière se manifeste sous un aspect discontinu ou corpusculaire. Elle est formée de particule (photons) d'énergie individuel E=hυ où h=6,625x10-34JS représente la constante de Planck, υ est la fréquence de vibration du rayonnement.
Cette théorie ne peut pas expliquer les phénomènes de diffraction ni d'interférence.
Aspect ondulatoire
- La lumière est une onde (onde lumineuse), constituée par un champ électrique E et un champ magnétique H perpendiculaire entre eux et perpendiculaire à la direction de propagation (onde électromagnétique)
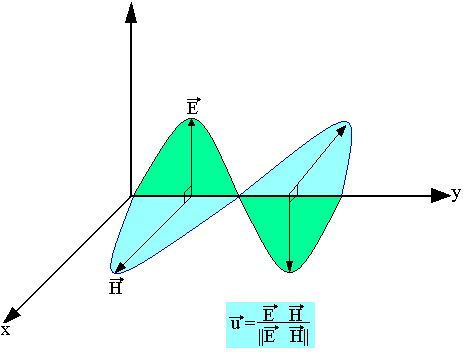
- Toutes les ondes lumineuses (visibles ou invisibles) ont la même vitesse de propagation dans le vide c=2993790Km/S2
- Onde monochromatique toute onde électrique ayant une fréquence unique, c'est-à-dire se manifestant par une seule couleur, c'est la lumière saine (différente de la lumière composée). La lumière est généralement sinusoïdale donc la période T=1/f=1/v dépend de la source et non du milieu de propagation
- Vitesse de propagation V(M,u): Pour V(M,U)=V(u), on dit que le milieu est homogène (même propriété physique en tous les points du milieu).
Pour V(M,U)=V(M), le milieu est dit isotope (même propriété physique dans toutes les directions). La longueur d'onde est: λ=VT et l'équation de l'onde monochromatique est de la forme
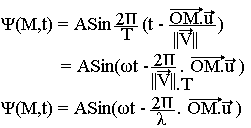
- Indice de réfraction d'un milieu homogène: V(M,u)=V(u)
V est la vitesse de propagation de la lumière dans un milieu 1 et c est la vitesse de propagation de la lumière dans le vide tel que C>V. On définit donc n=c/V>1, comme l'indice de réfraction du milieu 1. n est une fonction notée n(M), en général et pour un milieu homogène n=cste
Remarques:
Remarque 1: Dans un milieu donné la vitesse de la lumière dépend de la radiation considérée (milieu dispersif).
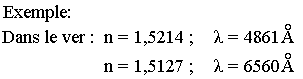
Remarque 2: Si le milieu n'est pas homogène, l'indice de réfraction devient une fonction scalaire du point n=f(x, y, z).
Remarque 3: Une source de lumière qui émet dans le vide, une radiation de longueur d'onde donne dans un milieu homogène d'indice n, une longueur d'onde telle que:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale