Stigmatisme d'un point aplanétisme

Stigmatisme rigoureux

Considérons deux points A et A' séparé par un système optique (S), un rayon passant par A repassera par A' si le principe de FERMAT est satisfait.

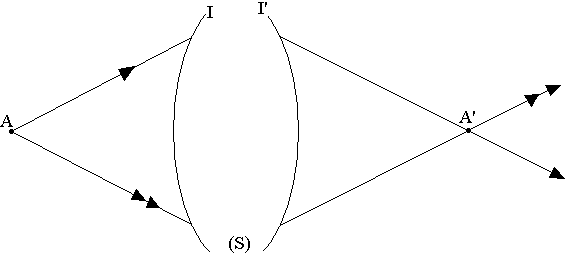
En général ce rayon est unique mais pour certain cas il existe une infinité de rayon permettant de joindre les points A et A'. Sur chacun de ces rayons le chemin optique (AII'A')=constante. En définitive le chemin optique ne dépend pas du rayon suivi, on dit qu'il y'a stigmatisme rigoureux.

Image d'un point

Si A et A' sont rigoureusement stigmatiques pour un système optique (S), on dit que A' est l'image de A (ou bien le conjugué de A) par le système.

Aplanétisme

Soit un système optique (S) admettant un axe de révolution considérons deux point A et A' de l'axe tel que (S) soit stigmatique aux points A et A'.