• La lumière est une onde (onde lumineuse), constituée par un champ électrique E et un champ magnétique H perpendiculaire entre eux et perpendiculaire à la direction de propagation (onde électromagnétique)
  
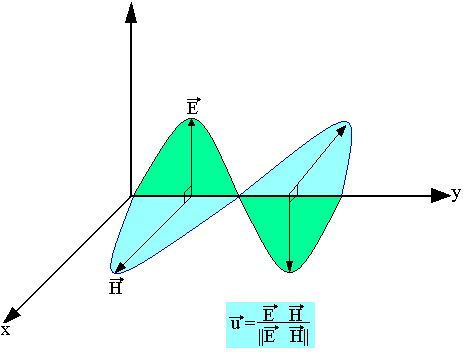
• Toutes les ondes lumineuses (visibles ou invisibles) ont la même vitesse de propagation dans le vide c=2993790Km/S²
• Onde monochromatique toute onde électrique ayant une fréquence unique, c'est-à-dire se manifestant par une seule couleur, c'est la lumière saine (différente de la lumière composée). La lumière est généralement sinusoïdale donc la période T=1/f=1/v dépend de la source et non du milieu de propagation
• Vitesse de propagation V(M,u): Pour V(M,U)=V(u), on dit que le milieu est homogène (même propriété physique en tous les points du milieu).
  Pour V(M,U)=V(M), le milieu est dit isotope (même propriété physique dans toutes les directions). La longueur d'onde est: λ=VT et l'équation de l'onde monochromatique est de la forme
  
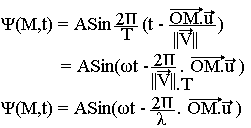
• Indice de réfraction d'un milieu homogène: V(M,u)=V(u)
  V est la vitesse de propagation de la lumière dans un milieu 1 et c est la vitesse de propagation de la lumière dans le vide tel que C>V. On définit donc n=c/V>1, comme l'indice de réfraction du milieu 1. n est une fonction notée n(M), en général et pour un milieu homogène n=cste

Remarques:

Remarque 1: Dans un milieu donné la vitesse de la lumière dépend de la radiation considérée (milieu dispersif).

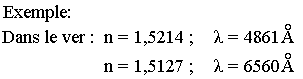
Remarque 3: Une source de lumière qui émet dans le vide, une radiation de longueur d'onde donne dans un milieu homogène d'indice n, une longueur d'onde telle que:

---

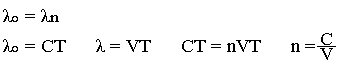
Propagation rectiligne de la lumière

Expérience

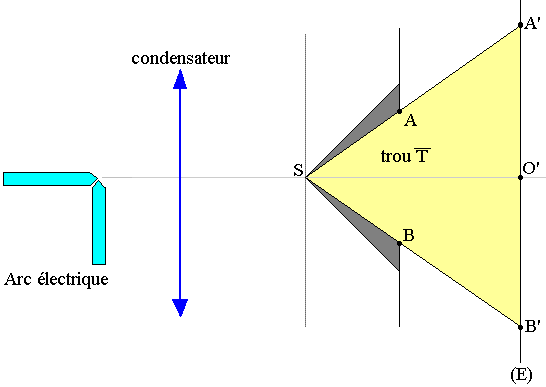
Constats:

Enoncés

Lois de Descartes-SNELL

Phénomène de réfraction

Considérons deux milieux transparents homogènes et isotopes séparés par une surface quelconque S.

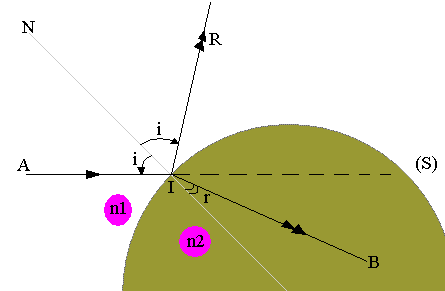
L'expérience montre que le rayon lumineux A passant du milieux (1) au milieu (2) subit d'un changement de direction au point i (phénomène de réfraction)
AI = rayon incident
IB = rayon réfracté
IR = rayon réfléchi
AIN = plan d'incidence
i = angle d'incidence
i = angle de réflexion
r = angle de réfraction

Lois de DESCARTES

L₁: Le rayon réfracté est dans le plan d'incidence.
L₂: Il existe un rapport constant entre les sinus des angles d'indice de réfraction. n₁Sin(i)=n₂Sin(r)
L₃: Le rayon est dans le plan d'incidence.
L₄: L'angle de réflexion est égal à l'angle d'incidence.

Le principe de FERMAT

Surface d'onde-vecteur d'onde-rayon lumineux

Une vibration étant représentée par la fonction S=aCos(ωt-þ) en un pont M(x, y, z) à l'instant t. On appelle surface d'onde l'ensemble des points qui à un instant t ont la même élongation.
Les surfaces d'onde admettent en chacun de leurs points un vecteur K=gradþ appelé vecteur d'onde.
Les rayons lumineux sont des trajectoires orthogonales aux surfaces d'onde.

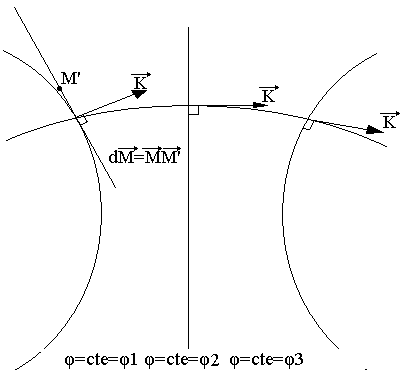
Remarque: Soit une surface d'onde S définie par þ(x, y, z)=constante. Pour un déplacement élémentaire dM du point M, on a:

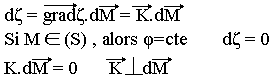
Chemin optique

Soit un rayon lumineux passant de A vers B et ne propagent à la vitesse V

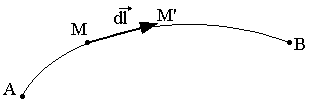
Considérons deux points M et M' le long de ce rayon MM'=dl
Le temps que met l'onde pour passer de M à M' est:

Pendant ce même temps dt l'onde aurait parcouru dans le vide dL=cdt=cn(M).dl/c=n(M).dl
On appelle chemin optique de A à B, le long du trajet r. La distance notée:

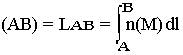
Propriétés

• Si v désigne la fréquence de la vibration lumineuse considérée et C la vitesse de la lumière dans le vide, alors:
  
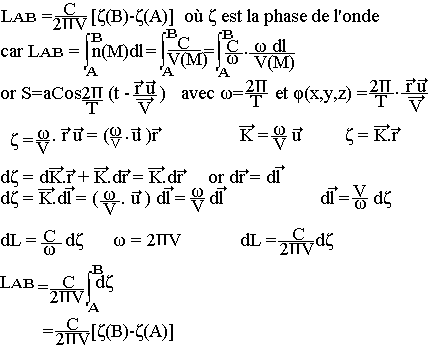
• Le chemin optique est une grandeur algébrique.
• Le chemin optique entre deux surfaces d'onde est indépendant du rayon choisi.
  

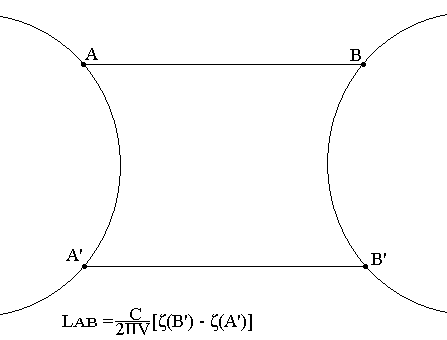
Enoncé du principe de FERMAT

Parmi les trajets possibles et infiniment voisins pour aller de A à B fixe, le trajet effectivement choisi est celui pour lequel le chemin optique est minimal.

Equation de la trajectoire des rayons lumineux

Considérons un trajet lumineux passant par deux points A et B fixe dans un milieu homogène. Soit M(x, y, z) un point courant de ce trajet, on doit écrire:

Supposons que la trajectoire des rayons lumineux soit une courbe dans l'espace donc l'équation peut se mettre sur la forme:

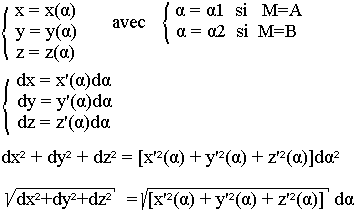
Où x', y’, z’ sont les dérivées de x, y, z. Le problème consiste donc à minimiser la grandeur On dit qu'il s'agit d'un problème variable ordinaire.

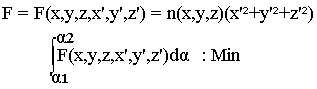
On démontre et nous admettons que ce problème est équivalent à la résolution du système d'équation suivant appelé équation d'Euler Lagrange

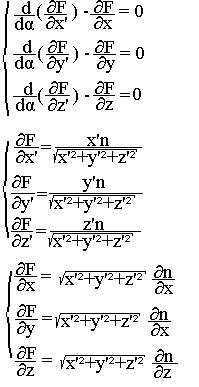
Introduisons le vecteur unitaire tangent à la trajectoire lumineux.

L'équation précédente permet d'obtenir l'équation de la trajectoire sur la forme suivante r=r(s) où s est l'abscisse curviligne et les points A et B sont fixes.

Conséquence:

Trajectoire des rayons lumineux dans un milieu homogène:

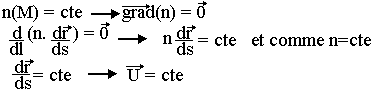
Le vecteur unitaire tangent à la trajectoire est un vecteur constant c'est-à-dire la trajectoire est une droite, et c'est la droite AB.

Enoncé:

Dans un milieu homogène les rayons lumineux sont des droites et le chemin optique AB est donné par nAB.

Stigmatisme d'un point aplanétisme

Stigmatisme rigoureux

Considérons deux points A et A' séparé par un système optique (S), un rayon passant par A repassera par A' si le principe de FERMAT est satisfait.

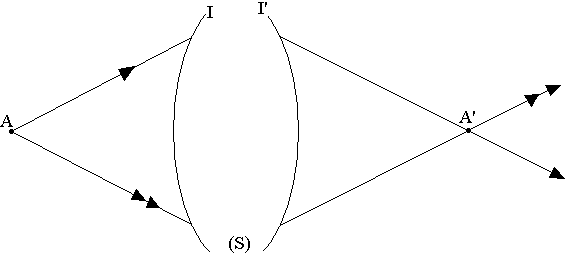
En général ce rayon est unique mais pour certain cas il existe une infinité de rayon permettant de joindre les points A et A'. Sur chacun de ces rayons le chemin optique (AII'A')=constante. En définitive le chemin optique ne dépend pas du rayon suivi, on dit qu'il y'a stigmatisme rigoureux.

Image d'un point

Si A et A' sont rigoureusement stigmatiques pour un système optique (S), on dit que A' est l'image de A (ou bien le conjugué de A) par le système.

Aplanétisme

Soit un système optique (S) admettant un axe de révolution considérons deux point A et A' de l'axe tel que (S) soit stigmatique aux points A et A'.