Le principe de FERMAT

Surface d'onde-vecteur d'onde-rayon lumineux

Une vibration étant représentée par la fonction S=aCos(ωt-þ) en un pont M(x, y, z) à l'instant t. On appelle surface d'onde l'ensemble des points qui à un instant t ont la même élongation.
Les surfaces d'onde admettent en chacun de leurs points un vecteur K=gradþ appelé vecteur d'onde.
Les rayons lumineux sont des trajectoires orthogonales aux surfaces d'onde.

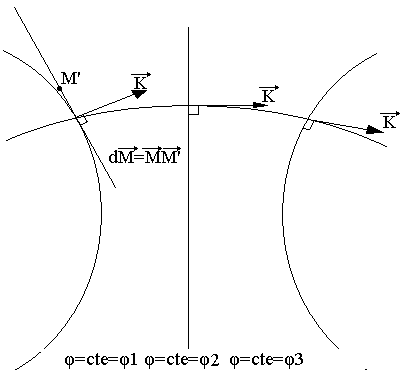
Remarque: Soit une surface d'onde S définie par þ(x, y, z)=constante. Pour un déplacement élémentaire dM du point M, on a:

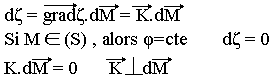
Chemin optique

Soit un rayon lumineux passant de A vers B et ne propagent à la vitesse V

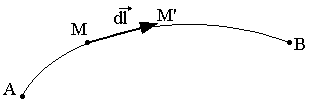
Considérons deux points M et M' le long de ce rayon MM'=dl
Le temps que met l'onde pour passer de M à M' est:

Pendant ce même temps dt l'onde aurait parcouru dans le vide dL=cdt=cn(M).dl/c=n(M).dl
On appelle chemin optique de A à B, le long du trajet r. La distance notée:

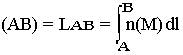
Propriétés

• Si v désigne la fréquence de la vibration lumineuse considérée et C la vitesse de la lumière dans le vide, alors:
  
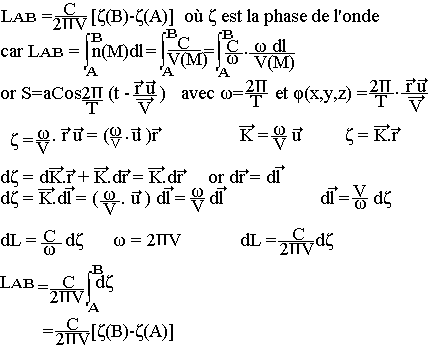
• Le chemin optique est une grandeur algébrique.
• Le chemin optique entre deux surfaces d'onde est indépendant du rayon choisi.
  

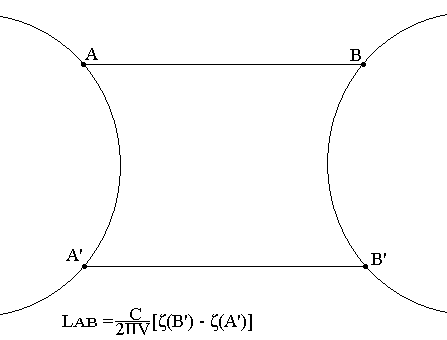
Enoncé du principe de FERMAT

Parmi les trajets possibles et infiniment voisins pour aller de A à B fixe, le trajet effectivement choisi est celui pour lequel le chemin optique est minimal.

Equation de la trajectoire des rayons lumineux

Considérons un trajet lumineux passant par deux points A et B fixe dans un milieu homogène. Soit M(x, y, z) un point courant de ce trajet, on doit écrire:

Supposons que la trajectoire des rayons lumineux soit une courbe dans l'espace donc l'équation peut se mettre sur la forme:

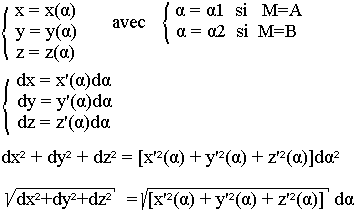
Où x', y’, z’ sont les dérivées de x, y, z. Le problème consiste donc à minimiser la grandeur On dit qu'il s'agit d'un problème variable ordinaire.

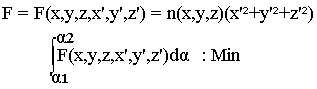
On démontre et nous admettons que ce problème est équivalent à la résolution du système d'équation suivant appelé équation d'Euler Lagrange

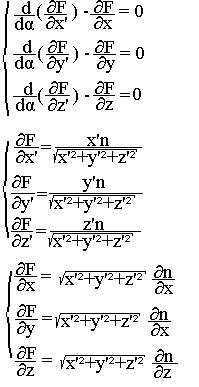
Introduisons le vecteur unitaire tangent à la trajectoire lumineux.

L'équation précédente permet d'obtenir l'équation de la trajectoire sur la forme suivante r=r(s) où s est l'abscisse curviligne et les points A et B sont fixes.

Conséquence:

Trajectoire des rayons lumineux dans un milieu homogène:

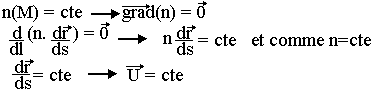
Le vecteur unitaire tangent à la trajectoire est un vecteur constant c'est-à-dire la trajectoire est une droite, et c'est la droite AB.

Enoncé:

Dans un milieu homogène les rayons lumineux sont des droites et le chemin optique AB est donné par nAB.