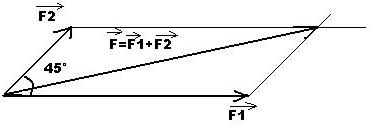L'action exercée par un ouvrier pour soulever un sac, celle d'un footballeur qui met un ballon en mouvement, celle d'un pousseur qui tire son porte-tout, celle d'un garçon qui tord une tige métallique. Toutes ces actions nous montrent que ces différentes personnes exerces chacune une force.
On appelle force, toutes action capable de provoquer ou de modifier un mouvement, de maintenir en équilibre ou de déformer un corps.
La force n'est pas visible ni papable, on ne la reconnaît que par ses efforts
Les effets d'une force
On distingue 2 effets:
- Un effet dynamique: lorsqu'une force peut provoquer ou modifier le mouvement d'un corps, elle est dite à effet dynamique
- Un effet statique: Une force est dite statique lorsqu'elle peut causer la déformation d'un corps ou le maintenir en en équilibre. Exemple de force statique: l'arrêt d'un ballon par un gardien de but
Classification des forces
On distingue les forces de contact et les forces à distance (ou force de champ).
On appelle champ toute région de l'espace soumise à l'influence d'une force.
Les forces de contact
Ce sont des forces qui s'exercent par contact direct ou indirect entre le producteur de la force (agent) et l'objet (receveur). Exemple de force de contact: la force musculaire, la force élastique, la force pressante, la force de frottement(ou adhérence), la force de liaison.
La force à distance ou force de champ
Ce sont des forces qui s'exercent sans qu'un contact direct ou indirect ne soit nécessaire entre l'agent et l'objet. Exemple de force de champ: force magnétique, force électrique, force de pesanteur.
Notation et représentation d'une force
En général, on note une force par une lettre majuscule surmontée d'une fiche.
Une force peut-être représentée par un segment de droite orienté
Caractéristique d'une force
Toute force est caractérisée (distinguée d'une autre force) par 4 éléments qui sont:
- Son point d'application: en général c'est le centre de gravité de l'objet
- Sa direction (ou droite d'action) ou support, on distingue 3 directions: la direction horizontale, la direction verticale et la direction oblique
- Son sens: C'est celui du mouvement qu'elle tant à produire, si le sens du mouvement est celui de la force et est dite motrice. Si le sens de la force est contraire à celui du mouvement, la force est dite résistante.
- Son intensité (ou module): c'est la valeur de la force, elle est mesurée à l'aide d'un appareil appelé le dynamomètre, l'unité de l'intensité est le Newton (N)
L'intensité n'est jamais surmontée d'une flèche Exemple: F=5N
Pour représenter graphiquement une force, on la représente par un vecteur (segment de droite orienté), ce vecteur a pour origine le point d'application de la force, pour direction la droite d'action de la force, le même sens que la force, sa longueur ou norme est proportionnel à l'intensité de la force.
La norme d'une force est la longueur de la flèche qui la représente. Pour représenter une force, il faut toujours connaître l'échelle de représentation.
Exemple:
Représenter la force F, l'intensité 50N, on donne 1cm correspond à 10N
Résolution:
on donne 1cm → 10N
l? ← 50N
l=(1x50)/10 =5cm
5cm
Norme de F égale à 50cm
Autres types de forces
- Forces colinéaires:
Des forces sont dites colinéaires lorsqu'elles ont la même direction - Forces opposées:
2 forces sont dites opposées lorsqu'elle ont la même direction, la même longueur et de sens contraire.
Somme géométrique de plusieurs forces (ou forces résultantes)
La somme géométrique de plusieurs forces F1, F2, F3, ...Fn est la force qui produit sur un corps les mêmes effets que les forces F1, F2, F3, Fn agissant ensemble, on note alors:
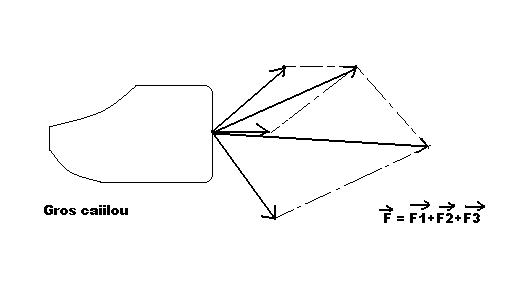
Cas des forces colinéaires
Cas des forces colinéaires de même sens
Lorsque plusieurs forces sont colinéaires de même sens, l'intensité et la norme de leurs sommes géométriques sont respectivement égales à la somme arithmétique des intensités et des normes de ces forces.
Exemple:
Déterminez l'intensité de la somme géométrique et la norme des forces F1, F2, F3 tel que:
F1 = 10N
F2 = 7N
F3 = 15N
On donne l'échelle de représentation 2cm → 5N
Résolution:
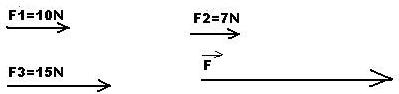
- Norme de la somme géométrique est: l=12,8cm
|
Norme de F1 |
Norme de F2 |
Norme de F3 |
Norme de F |
|
2cm → 5N |
2cm → 5N |
2cm → 5N |
2cm → 5N |
- Intensité de la somme géométrique de F
F=F1+F2+F3
AN: F=10+7+15=32N
F=32N
Cas des forces colinéaires n'ayant pas le même sens
Pour calculer l'intensité de la somme géométrique des forces colinéaires n'ayant pas toute un même sens, il faut d'abord se fixer soi-même un sens positif en suite on précède toutes les forces qui vont dans ce sens du signe +.
Pour celles qui vont dans le sens contraire, on précède leur intensité du signe -.
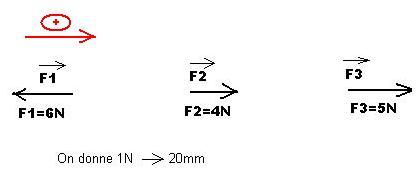
Déterminez le sens, la norme et l'intensité de la somme géométrique de ces 3 forces.
|
Intensité de la somme géométrique F |
||
|
F=F1+F2+F3 |
Autre choix |
Norme de F |
Equilibre d'un solide soumis à l'action de plusieurs forces colinéaires
Un solide soumis à plusieurs forces colinéaires ne peut rester en équilibre que si la somme géométrique de toutes ses forces à une intensité nulle. C'est-à-dire la somme des forces dirigées dans un sens est égale à la somme des forces dirigées dans le sens le sens contraire.

(A) est en équilibre si F1+F2+F3=F4+F5
Solide soumis à l'action de deux force concourantes
Pour trouver l'intensité de la somme géométrique de 2 forces concourantes, on procède par mesurage en suite on effectue une règle de 3.
Exemple:
Déterminez l'intensité de la force résultante de 2 forces F1 et F2, telles F1=24N; F2=16N; l'angle entre F1 et F2 mesure 45°. On donne 1 cm pour 10N.
Résolution
Calcul des normes.
|
Norme de F1 |
Norme de F2 |
|
1cm ==> 10N |
1cm ==> 10N |
Calculons l'intensité de F1 par mesurage
m=2,8cm
1cm ← 10N
3,8cm → F?
F=10x3,8/1 = 38
F=38N