Représentation des fonctions logiques
Une fonction logique peut se représenter sous 4 formes:
- La forme algébrique F = A + B
- La table de vérité
- D'un logigramme ou schéma d'implantation
- D'un tableau de Karnaugh
Représentation algébrique
C'est l'expression polynomiale d'une fonction logique constituée de la somme de plusieurs monômes des variables binaires. Elle peut se présenter sous forme d'une somme de produit:

Représentation sous forme d'une table de vérité
La table de vérité permet de représenter toutes les combinaisons possibles des variables binaires d'une fonction logique.
Représentation de la fonction "OU" à 2 variables dans une table de vérité
|
a |
b |
F = (a+b) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |

Pour représenter algébriquement f(a,b) à partir d'une table de vérité, on prend généralement les expressions (ou combinaison) qui donne f(a,b)=1.
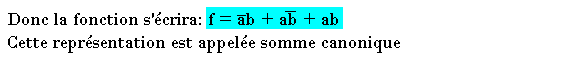
On peut également représenter la même fonction en prenant les expressions de ƒ(ab)=0 dans ce cas on fera le produit de la somme. Les variables sont au niveau bas: ƒ'= (a+b)(...+...)... Cette représentation s'appelle produit canonique.
Représentation sous forme de tableau de Karnaugh
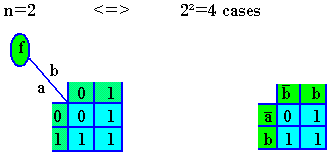
Le diagramme de Karnaugh est un tableau qui permet au même titre que la table de vérité la représentation d'une fonction logique. Pour une fonction à n variables, le tableau aura 2n cases. Chaque case représente la valeur de la fonction pour une combinaison de variables. On utilise le code Gray pour effectuer les combinaisons afin d'éviter le changement de plusieurs variables lors du passage d'une case à une autre.
Exemple de représentation de la fonction "OU" à variables dans le tableau de Karnaugh
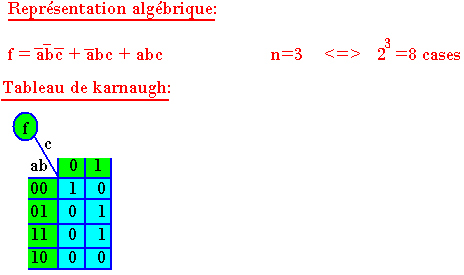
Exemple d'une représentation de la fonction logique à 3 variables dans le tableau de Karnaugh
Soit la fonction f représentée par la table de vérité suivante
|
a |
b |
c |
f |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Représentation sous forme d'un logigramme
Représenter une fonction logique sous la forme d'un logigramme revient à réaliser son schéma de câblage à l'aide des portes logiques.
Exemple 1:
Représenter le logigramme de la fonction f1=ab+cd
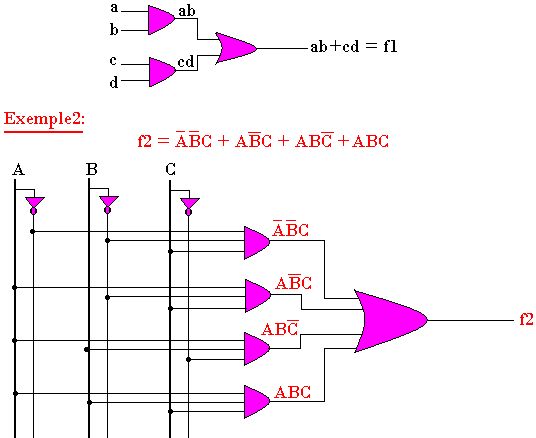
La simplification permet de réduire les expressions logiques sans toutefois modifier leur fonction. On peut alors utiliser soit la méthode de simplification logique soit par le tableau de Karnaugh.
Méthode de simplification algébrique
On utilise pour cette méthode les propriétés et théorèmes de Boole ainsi que les théorèmes de DEMORGAN.
Théorème de Boole
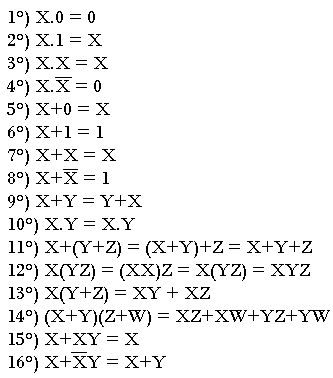
Théorème de DEMORGAN
Ce théorème permet de calculer le complément d'une expression.

Le théorème de DEMORGAN est utilisé lorsqu'il faut uniformiser les portes logiques d'un logigramme.
Exemple:
Réaliser le logigramme de la fonction suivante à l'aide des opérateurs "NAND" uniquement: f=A+BC
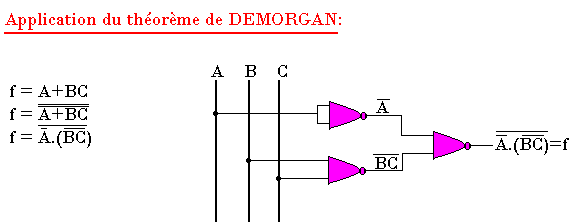
Méthode de simplification par tableau de Karnaugh
La simplification par tableau de Karnaugh se fait de la manière suivante:
- Remplir les cases du tableau par les 0 ou 1 selon l'état de sortie de la fonction.
- Faire des regroupements des cas contenants "1" adjacent par puissance de 2 (2, 4, 16, 32 ...)
- Chaque "1" doit appartenir à un ou à plusieurs regroupements.
- Simplification d'une variable se fait lorsqu'on change d'état au passage d'une colonne à une autre ou d'une ligne à une autre.
- La valeur d'un regroupement correspond enfin à la ou les variables qui restent inchangées.
Il faut avoir le plus grand nombre de "1" possible pour que la simplification soit optimale.
Application
Exemple 1:
Simplification par Karnaugh l'expression:
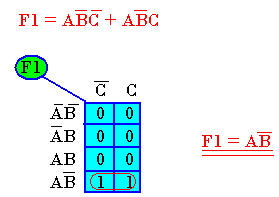
Exemple 2:
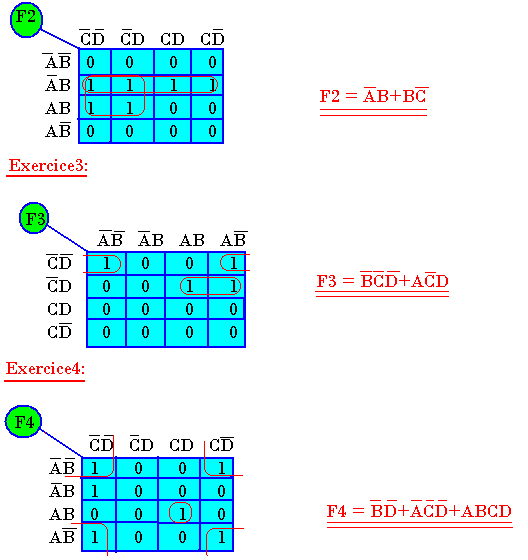
Simplifier l'expression contenue dans le tableau de Karnaugh ci-dessous
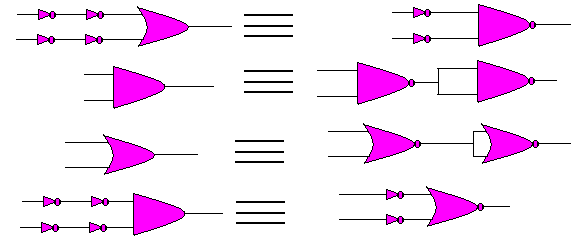
Universalité des portes NAND et NORD
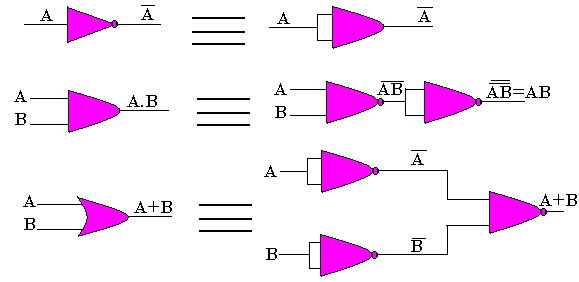
Fonction élémentaires avec les portes NAND
Fonction élémentaire avec les NOR
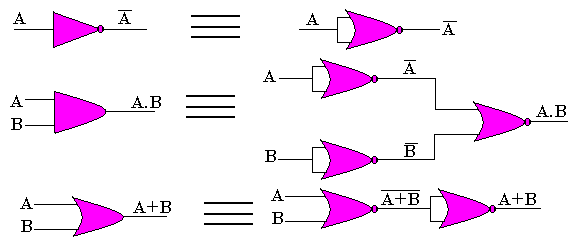
Lorsqu'on insère les doubles inverseurs aux entrées d'une porte "OU", la porte "ET" les 2 premiers inverseurs constituent une porte NAND. Lorsqu'on insère les doubles inverseurs aux entrées d'une porte "ET", la porte et les deux premiers inverseurs constituent une porte NOR.