Page 3 sur 4
Théorème de DEMORGAN
Ce théorème permet de calculer le complément d'une expression.
Le théorème de DEMORGAN est utilisé lorsqu'il faut uniformiser les portes logiques d'un logigramme.
Exemple:
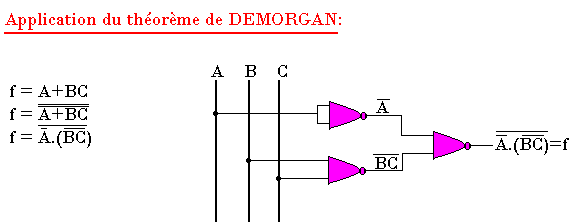
Réaliser le logigramme de la fonction suivante à l'aide des opérateurs "NAND" uniquement: f=A+BC
Méthode de simplification par tableau de Karnaugh
La simplification par tableau de Karnaugh se fait de la manière suivante:
- Remplir les cases du tableau par les 0 ou 1 selon l'état de sortie de la fonction.
- Faire des regroupements des cas contenants "1" adjacent par puissance de 2 (2, 4, 16, 32 ...)
- Chaque "1" doit appartenir à un ou à plusieurs regroupements.
- Simplification d'une variable se fait lorsqu'on change d'état au passage d'une colonne à une autre ou d'une ligne à une autre.
- La valeur d'un regroupement correspond enfin à la ou les variables qui restent inchangées.
Il faut avoir le plus grand nombre de "1" possible pour que la simplification soit optimale.
Application
Exemple 1:
Simplification par Karnaugh l'expression:
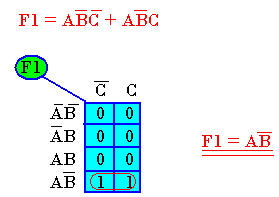
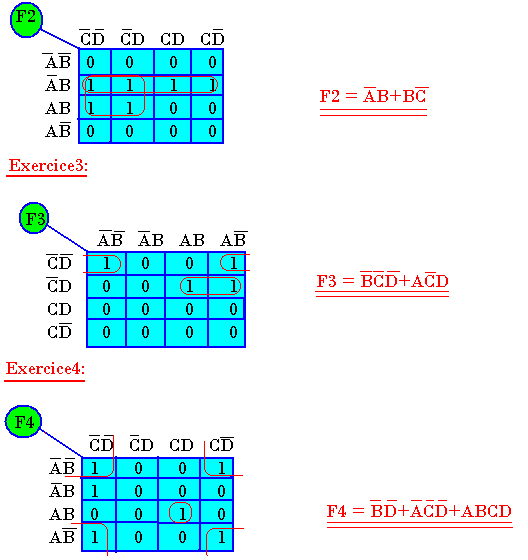
Exemple 2:
Simplifier l'expression contenue dans le tableau de Karnaugh ci-dessous
Concours d'entrée aux grandes écoles