Page 1 sur 4
Définition et représentation
Un système triphasé équilibré est un ensemble de 3 grandeurs de même dimension x1, x2, x3) tel que si
x1 = X1maxSin(ωt+Þ1)
x2 = X2maxSin(ωt+Þ2)
x3 = X3maxSin(ωt+Þ3)
on a:
- X1max = X2max = X3max
- x1, x2 et x3 régulièrement déphasés de 2IIm/3
Avec m=1 ou 2
On distingue deux types de système triphasé:
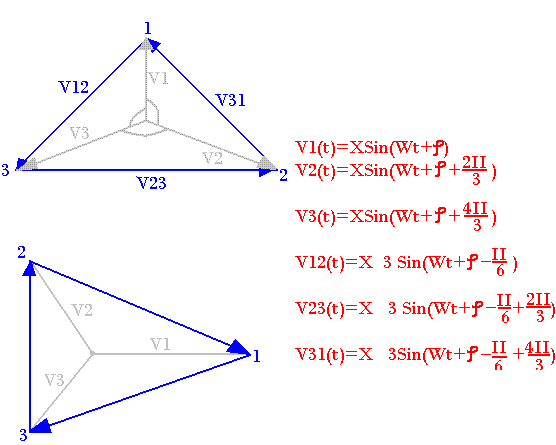
- Le système équilibré direct:
- x1(t) = X1maxSin(ωt-Þ)
- x2(t) = X2maxSin(ωt-Þ-2π/3)
- x3(t) = X3maxSin(ωt-Þ-4π/3)
Avec X1max = X2max = X3max = Xmax
- Système triphasé équilibré indirect
- x1(t) = X1maxSin(ωt-Þ)
- x2(t) = X2maxSin(ωt-Þ+2II/3)
- x3(t) = X3maxSin(ωt-Þ+4II/3)
Représentation
- Les systèmes triphasés directs
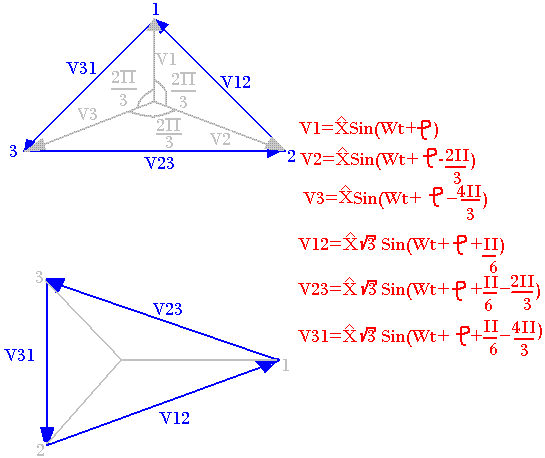
- Les systèmes triphasés indirects
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale