Détermination des asymptotes aux courbes

Problématique

La recherche des asymptotes aux courbes permet de déterminer l'allure des courbes de gain et de phase d'un amplificateur ou d'un quadripôle.

Exemple de tracé des asymptotes

Soit trois filtres F₁; F₂; F₃ de transmitance

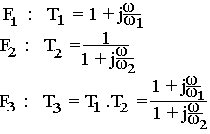
Soit à déterminer l'asymptote de la fonction de transfert T₂ pour cela par passage au gain

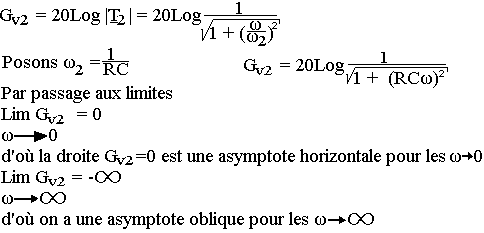
De ce fait il faut déterminer la pente, pour cela on peut considérer que ω=10ω₂ ou plus et par passage donc logarithmique, on aura:

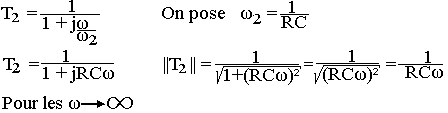
Par passage au gain
G_V2 = 20Log(1/RCω) = 20Log1 - 20Log(RCω) = -20Log(RCω)
A partir donc de cette expression, on remplace ω par 10ω₁ l'expression devient
-20Log(RC10ω₁) = -2Log10 - 20Log(RCω₁) = -20dB - 20Log(RCω₁)
A partir de cette expression on remarque que le gain G_V2 a pour variation DG_V2 et la pente de l'asymptote oblige est de -20dB/décade ceci représente un filtre de premier ordre.

Remarque:

Si on considère plutôt ω=2ω₂ alors par détermination on aura une pente de -6dB/octave. De même on peut considérer ω=100ω₂ le résultat du point de ce tracé sera identique de 10ω₀

Diagramme de Bode

On peut tracer facilement les diagramme de Bode en se referant différentes formes remarquables T₀, T₁, T₂, T₃, T'₃, T'₂. Dans ce cas on construit intervalle par intervalle en tenant compte des pulsations de coupure ω₀, ω₁, ω₂, ω₃, ω₄