Soit e(t) un signal d'entrée, s(t) un signal de sortie d'un système électronique. Supposons s₁(t) et s₂(t) des signaux de sortie correspondant aux signaux d'entrée e₁(t) et e₂(t).
Soient données T₁ et T₂ deux nombres algébrique, le système sera linéaire si au signal d'entrée
T₁e₁(t)+T₂e₂(t) ↔ T₁s₁(t)+T₂s₂(t)

Notion de dipôle

Le dipôle constitue l'élément le plus simple du circuit électronique, certains systèmes comprendront deux bornes à savoir une pour l'entrée et une pour la sortie.

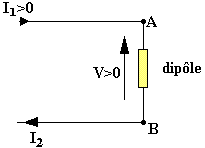
Il est parcouru par un courant I. Il est soumis à une différence de potentielle V=V_A-V_B entre A et B.

A: entrée du courant.
B: Sortie du courant.
Faisant varier le courant I, le potentiel VC aux bornes du dipôle varie. On eut donc tracer la courbe de variation I=ƒ(V) appelée courbe de caractéristique du dipôle.

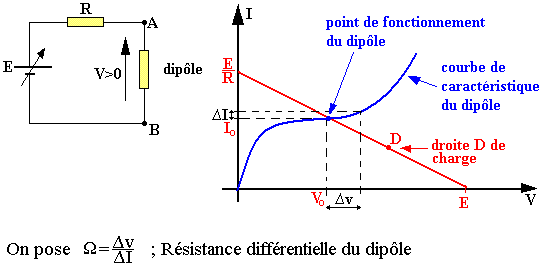
Point de polarisation du dipôle

Le dipôle associé à une source extérieure E et à une résistance R est traversé par un courant I₀. La tension en ce point est V₀, le point M caractérisé par le courant I₀ et la tension V₀ est appelée point de polarisation. Le point de fonctionnement se trouve à l'intersection de la caractéristique I=f(V) et de la droite d'équation I=-V/R+V/R, cette droite est obtenue par application de la loi d'ohm aux bornes de la résistance R ou droite appelée droite de charge.

Variation du point de fonctionnement

Toutes variation de la source E entraîne une variation du point de fonctionnement. Pour de faibles variations D_E de E. On pourra assimiler la courbe de caractéristique à sa tangente au point M.

Distorsion: cause de non linéarité série de Fourrier

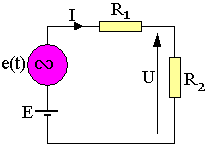
Les variations de la source E interviennent dans la mise en série d'une source e(t) associée à E. La deuxième source e(t) généralement sinusoïdale de pulsation ω, introduit aux bornes du dipôle des variations également sinusoïdales de fréquence multiples de ω. La plus faible étant appelée la fondamentale et égale à ou encore harmonique de rang 1 ou d'ordre 1. Ce phénomène se produit quant on s'écarte de la tangente de linéarité donnant naissance à des fonctions périodiques, satisfaisant aux conditions de Fourrier.
Les signaux rencontrés dans les systèmes électroniques sont généralement des tensions ou des courant de forme carrée, rectangulaire, triangulaire... ces fonctions seront généralement périodiques donc décomposable en série de Fourrier. L'étude d'un amplificateur passera alors à trois étapes:

Les quadripôles

A des rares exceptions près le dipôle ne peut pas jouer un rôle de circuit de commande car il n'a qu'un seul accès. Cette fonction sera effectuée par un plus complexe appelé quadripôle.

Un quadripôle est un réseau comportant deux bornes d'entrée et deux bornes de sortie:

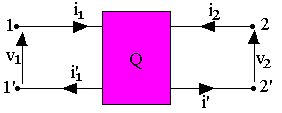
On note i₁ et i₂ les courants d'entrée et de sortie de même v₁ et v₂ tension d'entrée e de sortie. Le courant qui entre parmi les bornes d'entrée est égal au courant qui sort par l'autre borne de la même entrée de même pour la sortie. On adopte donc la convention des signes tel que indiqués sur le schéma. Cas particulier à retenir est celui où les bornes "1" et "2" sont confondues. On parle alors quadripôle. D'autre part un quadripôle peut être considéré comme association de deux dipôles dépendant l'un de l'autre. Ainsi la caractéristique d'entrée i₁=ƒ(v₁) dépend de l'état dans lequel se trouve la sortie et réciproquement. Ce qui donne alors deux relations: i₁=f(v₁,i₂,v₂) ; i₂=f(v₂,i₁,v₁)

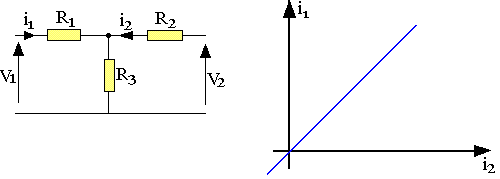
En général ces relations ne sont pas linéaires, encore moins exprimables algébriquement. Dans la pratique le comportement du quadripôle sera représenté par un double réseau de caractéristique à savoir:

Le point de fonctionnement étant au tour de ce point dit point de repos sera supposé petit afin de satisfaire aux conditions de linéarisation du système.

Equation des quadripôles

Dans la recherche des variations des équations (1) et (2) utilisons la formule de TAYLOR limitée au premier ordre qui veut que:

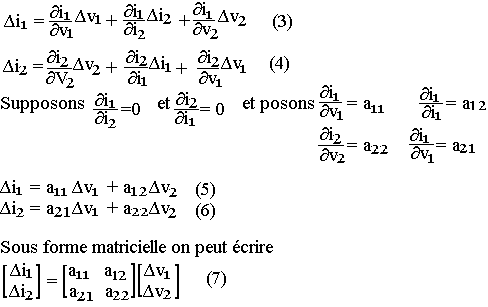
En basse fréquence on utilise souvent une représentation dite hybride avec les paramètres h_ij qui seront aussi des impédances que des admittances ou des nombres réels. Dans ce cas les équations du quadripôle s'écriront sous la forme:

Puisque les variations sont faibles, on peut écrire simplement que le système (8) et (9) devient:

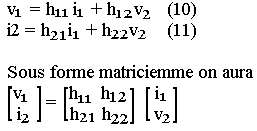
Quadripôle en petits signaux

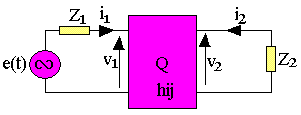
Nous supposons que les tension et courant sont faibles pour permettre la linéarisation des signaux. Le quadripôle Q étant caractérisé par les paramètres hybrides h_ij, il est alimenté par une f.e.m sinusoïdale e(t) d'impédance Z₁ et chargée par Z₂. Les équations régissant du circuit sont:

Les paramètres h_ij sont les caractéristiques du quadripôle et sont donc fonction des éléments qui le compose. La méthode d'étude consistera à représenter Q par son schéma équivalent à partir des définitions du paramètre h_ij. A ce titre on rappelle que h₁₁=(v₁/i₁)_v2=cste ; h₁₂=(v₁/v₂)_i1=cste ; h₂₁=(i₂/i₁)_v2=cste ; h₂₂=(i₂/v₂)_i1=cste
On obtient donc le schéma équivalent suivant:

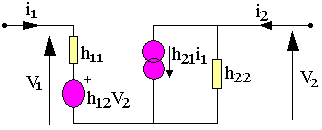
A partir des expressions ci-dessus déterminons l'impédance d'entrée du quadripôle Z₂=v₁/i₁
Dans (3) on a i₂=-v₂/z₂ (5)
(5) dans (2) -v₂/z₂=h₂₁i₁+h₂₂v₂
v₂=-h₂₁i₁/(1/z₂+h₂₂) (6)
(6) dans (1) donne:
z_e=h₁₁[1-h₁₂h₂₁/h₁₁(h₂₂+1/z₂)]
L'impédance de sortie z_s=v₂/i₂

(4) dans (1) donne
e(t)-z₁i₁=h₁₁i₁+h₁₂v₂ ↔ i₁ = e(t)/(z₁+h₁₁) - h₁₂/(z₁+h₁₁) (7)

(7) dans (2) donne
i₂ = h₂₁e(t)/(z₁+h₁₁) - h₂₁h₁₂v₂/(z₁+h₁₁ + h₂₂v₂
v₂=Þi₂+v₂₀ ; Þ=1/(h₂₂-h₂₁h₁₂/(z₁+h₁₁)
Dans la recherche des impédances de sortie nous allons supposer l'entrée en court-circuit (v₂₀=0)

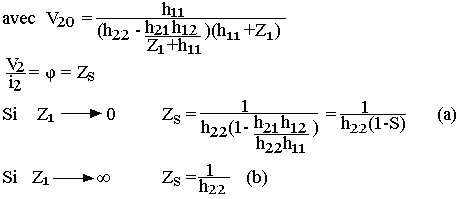
Dans le cas (a), on dira que le quadripôle a été attaqué par une source de tension.
Dans le cas (b) on dira que le quadripôle a été attaqué par une source de courant.
Le gain en tension sera G_v=v₂/v₁