Alternateur

Calcul de la f.e.m dans un enroulement

Un enroulement est formé à partir de n conducteur et comporte n/2 spires. La f.e.m induite dans une des spires est e=-dÞ/dt ; Þ=Þ_maxCosPrt. Si la machine a plusieurs paires de pôle: Þ_*=Þ_maxCosPrßt.
Nous savons par ailleurs que e à la sortie doit être e₁=ÊSinωt avec ω=2IIf par identification on a: e₁=E(2^½)Sinωt=Þ_maxPrSinPrt
E₁ = 4,44(P.2IIn)Ø_max
E₁ = 4,44PrØ_max
Pour n conducteurs en série mais par courant N/2 spires.
E_T = 2,22P_nN.Ø_max
Par ailleurs un enroulement est doté de n conducteurs série comportant N/2 spires (stator réel). La f.e.m induite est fonction du nombre de conducteur et sera noté
E_T. E_T étant la f.e.m induite dans une spire K=2,22 cœfficient de Kapp
E_T = K.P.n.Ø_max avec :

Dans le cas d'un alternateur triphasé, ces résultats s'appliquent à chaque enroulement de la machine. Il donne donc la valeur efficace de la tension simple si les enroulements sont en étoile et valeur efficace composées si les enroulements sont en triangle, la fréquence de rotation sera: f=P.n

Model élémentaire d'un enroulement

Représentation

Pour rendre compte du fonctionnement en régime permanant d'un alternateur débitant dans un réseau équilibré, à chaque enroulement de la machine on fait correspondre le model équivalent de la figure ci-contre.

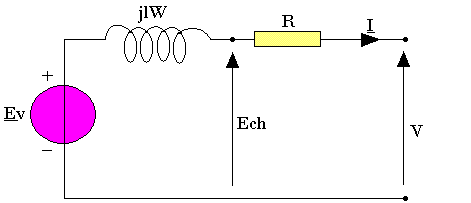
Equation:

E_v - jLωI - R.I - V = 0
V = E_v - I(JLω+R)
Il comporte une source de tension, une inductance L et une résistance R.

Diagramme synchrone de phase: diagramme de BENN ESGHEN BURG

Hypothèse:

• Le circuit magnétique est non saturé.

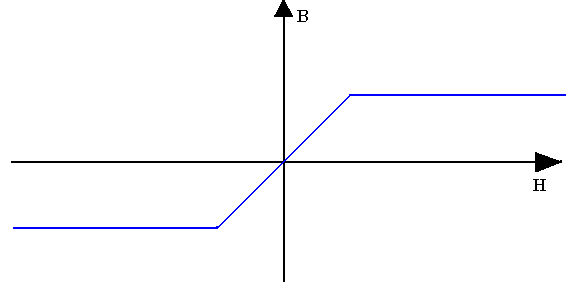
• Le flux en charge est égal au flux inducteur à vide plus celui dû à la réaction magnétique.

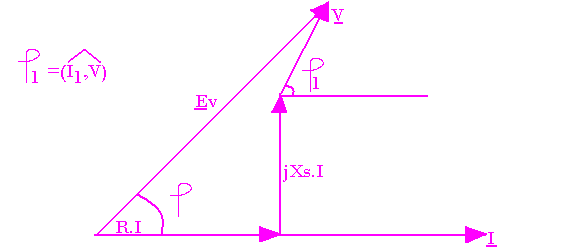
BENN admet que E dû à la réaction magnétique d'induit (Ø_a) désignée par LWI correspond à X_sI
Ø_ch=Ø_V+Ø_a ; E_ch=E_V+E_a
E_ch = E_v - jX_sI ; E_v = R.I + jX_sI + V

Détermination des éléments de BENN (X_s ; R_s)

Pour déterminer ces éléments nous procéderons notamment à l'essaie en court-circuit.

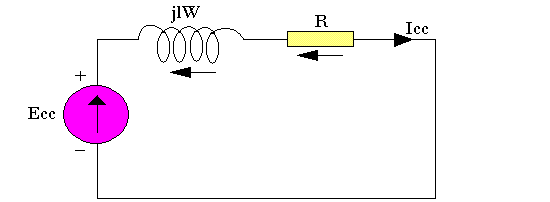
-E_Cc + jL.ω.I_CC + R.I_CC = 0 ↔ E_CC = R.I_CC + jL.ω.I_CC
E_CC = (R + jL.ω)I_CC

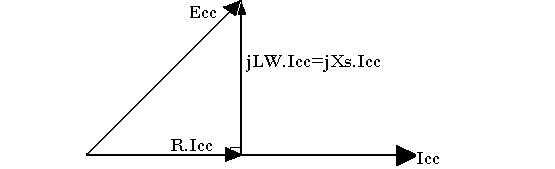
E²_CC = (R.I_CC)² + (X_s.I_CC)² ↔ E²_CC = (R² + X²_s)I²_CC
E2_CC/I²_CC = R² + X²_S
Or X_S >> R
E²_CC/I²_CC = R² + X²_s d'où finalement
X²_s = E²_CC/I_CC ↔ X_s = E_CC/I_CC
On peut déduire R soit par Z²=R²+X²_s
R = (Z² - X²_s)^½
Soit par la méthode volt-ampérométrique.

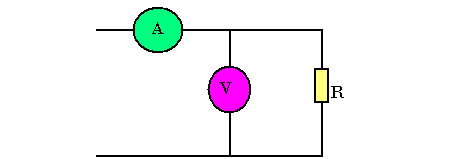
Bilan de puissance et rendement

Puissance

L'alternateur reçoit une puissance mécanique notée P_méca qui lui est fournie par le moteur d'entraînement P_méca=T_mec.r où T_méca est le couple électromagnétique du moteur, donc il restitue une puissance électrique à une charge.
Puissance utile:
P_u = 3^½U.I.CosÞ (3 phases)
P_u = U.I.CosÞ (une phase)
U est la tension composée, I le courant de ligne.
NB: Lorsque l'alternateur n'est pas auto excitée ou lorsque l'inducteur n'est pas constitué d'un aimant permanant, il faut l'alimenter en courant continu, donc lui donner une puissance électrique. On aura P=Ui=ri²
U: tension aux bornes de l'inducteur
i: Courant dans l'inducteur

Rendement

n_3ø = P_u/P_a = 3^½.U.I.CosÞ/(T_méca.r+U.i)
n_1ø = U.I.CosÞ/(T_méca.r+U.i)

Exercice 1:

Un alternateur triphasé tourne à 200tr/mi et produit une f.e.m de fréquence f=50Hz.
Calculez le nombre de pôle du stator.

Exercice 2:

Un alternateur 1ø à vide à aimant permanant fournit une f.e.m=220V lorsque la roue polaire tourne à 500tr/min.
Quel est la f.e.m si cet alternateur tourne à 600tr/min

Bilan de puissance

Dans l'alternateur, il existe 4 types de pertes:

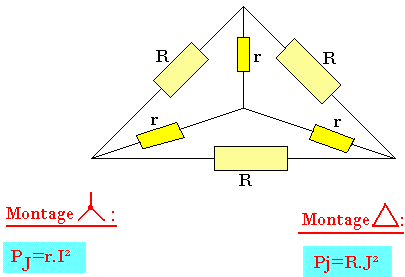
Rendement total:

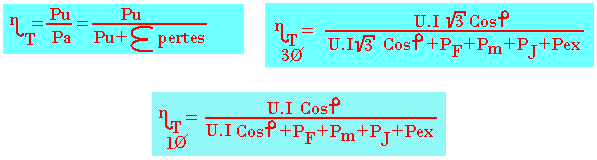
Détermination des pertes mécaniques

Cette détermination se fait à l'aide des essais sur l'alternateur.
Perte mécanique: On entraîne l'alternateur à vitesse nominale sans excitation et à vide. La puissance que lui fournit le moteur compense bien les pertes mécaniques. On a donc P_m égale n₁p₁. n rendement de la transmission.
En ce moment le courant d'excitation i est nul, i_e=I=0. Le rendement est nul.
Perte fer: On entraîne l'alternateur à vitesse nominale et à vide, cette fois-ci avec une excitation fournie par une source extérieure et qui permet à l'alternateur de délivrer sa tension nominale. La puissance absorbée par le moteur P₂ a un rendement n₂ compense à la fois les pertes mécaniques et les pertes fer.
P_m + PF = P₂n₂
P_F = P₂n₂ - P₁n₁