Généralités
Filtrer un signal c'est:
- L'identification de toutes les fréquences qui sont contenues dans le signal en fonction de leur amplitude
- Procéder à une élimination des signaux.
La transformée de FOURRIER discrète et la transformée en Z constituent les principales méthodes utilisées dans le traitement numérique des signaux. Dans ce cours nous ferons usage de ces deux méthodes et nous nous limiterons au système binaire invariant. Lorsqu'un tel système fréquentielle d'un signal, il est appelé filtre numérique et l'opération qui consiste à modifier cette distribution est appelé filtrage numérique.
Principes généraux
Les bases mathématiques
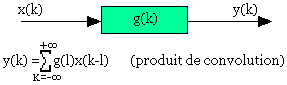
La réponse fréquentielle ou réponse harmonique G(f) d'un système linéaire invariant est lié aux transformées de FOURRIER des signaux d'entrée et de sortie par la relation bien connue.
![]()
X(f): transformée de FOURRIER de l'excitation
Y(f): transformée de FOURRIER du signal de sortie du système.
Domaine fréquentiel: Amplitude en fonction de la fréquence
Dans le domaine temporel: Amplitude en fonction du temps.
Classification des filtres numériques
Le problème général du filtrage numérique est d'élaborer un système linéaire invariant possédant une réponse fréquentielle de désirer et se prêtant à une réalisation facile.
Objectif : système invariant
Contrainte : fréquence fixée; facilité de réalisation
Pour que le système soit réalisable, il faut qu'il soit stable et causal. Le nombre d'opération à réaliser doit être limité. On distingue donc deux catégories de filtre numérique:
- Les filtres à réponse impulsionnelle infinie (R.I.I) pour lesquels les échantillons de g(k) sont non nuls pour k0<k<+∞
- Les filtres à réponse impulsionnelle (R.I.F) pour lesquels les échantillons de g(k) sont non nuls pour k0<k<k0+(L-1)
Une autre classification tient compte des moyens mis en oeuvre.
- La réalisation transversale ou non récursive dans ce cas le système est réalisée de manière non récursive.
- La réalisation récursive: le filtre est réalisé au moyen d'une équation haute différence.
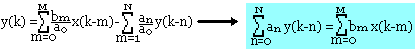
Utilisation de la transformée de FOURRIER
Qui donne une autre méthode de classification
La transformée de FOURRIER discrète peut être utilisée en prenant:
Transformée de FOURRIER de X(n)=F[x(k)] ; Y(n)=G(n).X(n) ; y(k)=F[Y(n)]
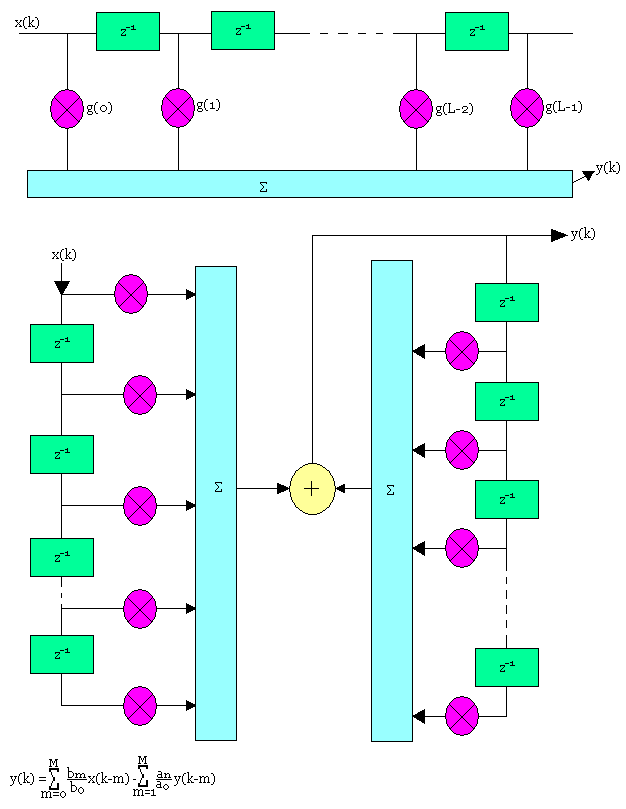
Structure de réalisation
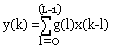
En examinant la relation ci-dessous, on remarque que le filtrage est effectué à l'aide de trois opérations:
- Le décalage de 1
- La multiplication
- La sommation
Echantillonnage
La première dans une modulation numérique consiste à prélever périodiquement des échantillons du signal analogique primaire. On montre que si la fréquence d'échantillonnage est assez élevée, il est possible de reconstituer le signal primaire sans altérer le signal qu'il contient.
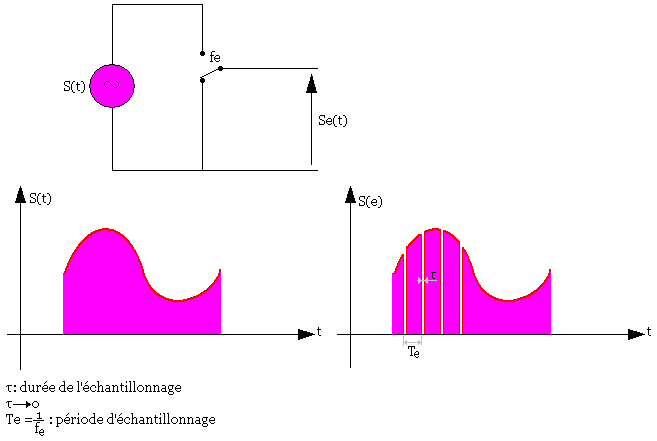
Expression mathématique
Le signal échantillonné peut être considéré comme étant le produit du signal primaire par une fonction périodique E(t) de période Te. Se(t)=S(t).E(t)
L'échantillonnage est équivalente à une modulation d'amplitude du signal S(t) par un train d'impulsion d'amplitude et période constante d'où le nom de Post Amplitude Modulation (PAM)
S(t) est un signal analogique (signal primaire non modulé)
E(t) train d'impulsion d'amplitude et de période constante.
C'est un signal discret disposant des énergies localisées à des instants précis. On peut le considérer comme le signal rectangulaire. Se)t)=S(t)E(t) : signal modulé en Amplitude disposant des énergies localisée.
La porteuse est un train d'impulsion.
Critère de NIKIST:
Fe: fréquence d’échantillonnage
B: bande passante du signal S(t)
Fe=2B: La fréquence la plus élevé de la bande de fréquence du signal S(t)
Système de transmission PAM
Le signal PAM est un signal échantillonné alors que le MIC est un signal numérique.
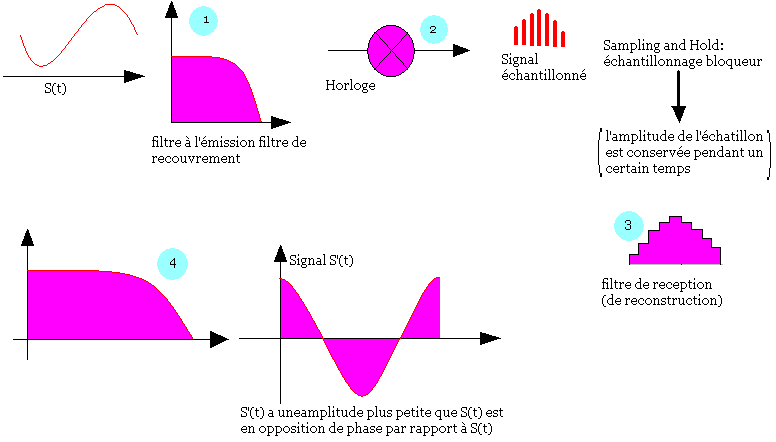
Modulation MIC
La modulation MIC (Modulation par Impulsion de Code) est une extension de la modulation PAM. Les échantillons analogiques PAM sont d'abord quantifiés en valeur discrètes puis elles son présentées en nombre entier selon un code.
Bruit de quantification
Le fait de remplacer les échantillons PAM qui peuvent prendre n'importe quelle valeur dans chaque intervalle par les valeurs discrètes d'échantillon dans cet intervalle est à l'origine d'erreur. Cette erreur est due au bruit de quantification. On mesure se bruit par le rapport signal sur bruit (S/B)q
(S/B)q = (Puissance du signal)/(Puissance du bruit)
(S/B)q = E[S(t)2]/E[Y(t)-S(t)]2
E : Moyenne temporelle (Valeur moyenne)
S(t) → Signal analogique à l'entrée
Y(t) → Signal décodé à la sortie.
Loi de quantification uniforme
La quantification peut être linéaire ou non linéaire dans le cas de la quantification linéaire, tous les intervalles de quantification ont la même longueur.
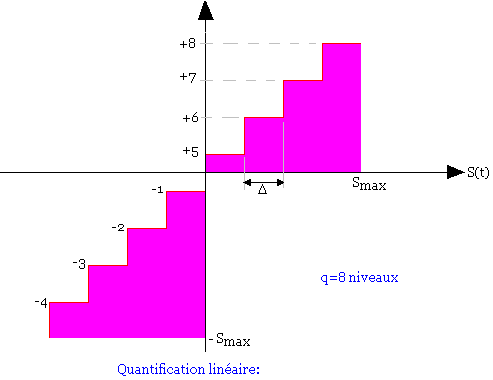
Le rapport signal sur bruit dans ce cas est:

Exemple:
Si nous avons un signal sinusoïdal d'amplitude Am.
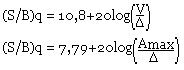
Exercice d'application:
Un signal sinusoïdal d'amplitude 1v doit être quantifié avec un rapport (S/B)q=30dB.
Combien faut-il d'intervalle de quantification et combien de bit faut-il pour coder chaque échantillon?
Utilisez les polarités positive et négative.

(S/B)q = 1,76 + 6,02n + 20log10(A/Amax)
A : amplitude du signal sinusoïdale.
Quantification non uniforme
Nous apercevons que pour les niveaux faibles (Amplitude A faible).
SQR : est faible alors qu'il est très élevé pour des niveaux forts, or nous souhaitons un SQR qui reste constant quelque soit le niveau pour cela on choisit delta variant en fonction du niveau, on procède de la manière suivante; le signal est d'abord compressé puis quantifié uniformément d'où le diagramme suivant:

On distingue deux lois de compression: la loi µ et la loi A.
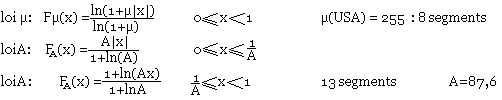
Compression selon la loi A
Nous pouvons x=U/Umax amplitude relative du signal dans laquelle U est l'amplitude du signal
Umax : amplitude max que peut prendre le signal.
La loi A s'écrit FA(x) = (1+ln|Ax|)/(1+lnA)
Le premier segment est un segment linéaire, le deuxième est un segment logarithmique. La pente du segment linéaire est appelée taux de compression.
C = A/(1+ln(A)
C=16 valeur choisie ; A=87,6
Pour une quantification linéaire on a la relation suivante.

On s'aperçoit donc que la partie logarithmique |x|>1/A l'objectif atteint à savoir un SQR indépendant de l'amplitude.
Paramètres importants:
Loi A: C=16 ; a=87,6 ; Q=28=256 niveaux
Segment linéaire SQR=3q2c2x2/2x2
Segment logarithmique SQR=3q2c2/A2 = constante
Compression selon la loi µ
Fµ(x) = ln(1+µx)/ln(1+µ)
µ = 255
c = µ/(ln(1+µ) = 46
Taux de compression à l'origine: les compressions sont faites pour équilibrer les voix téléphoniques.
Approximation de la loi A
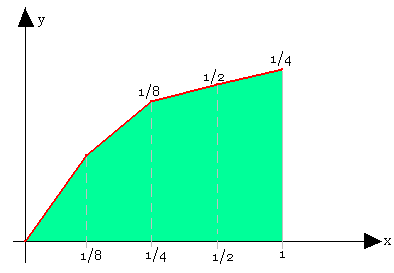
La solution technique pose beaucoup de problèmes pour la réalisation de la compression car il n'est pas toujours possible de trouver des éléments réciproques pouvant réaliser les deux opérations inverses. Actuellement la solution par compression numérique est beaucoup plus utilisée, elle consiste à approximer la loi A par une caractéristique polygonale à 13 segments linéaire. Les paries de ce segment sont dans une progression géométrique de raison ½.
Le premier segment de pente 16 c'est-à-dire taux de compression passe par l'origine.
Les caractéristiques sont les suivantes: La quantification est uniforme à l'intérieur de chaque segment et comporte 16 niveaux.
Dans le mot PCM codé à 8 bits le premier bit est un bit de signe, les 3 suivantes indiquent le numéro de segment et les 4 derniers bits le niveau dans chaque segment.
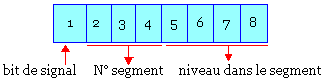
La numérisation ne produit pas de manière fidèle le signal analogique correspondant car il existe des erreurs de quantification dues aux valeurs approchées de la loi µ et de la loi A.
Téléphonie fixe:
Loi A à 13 segment= 18 KHz, quantification non uniforme à q=256 niveaux, mots MIS log2(q)=log(28)=8bits débit binaire par voie D=f0log2(q)=64bits/s
Télévision:
fe=13,3MHz , codage uniforme à 8 bits on a9 bits.
La télévision est un ensemble de moyen et de procédé technique permettant la transmission des images fixes ou animées ainsi que le son qui est associé sur des distances importantes.
La télévision
La chaîne de télévision est constituée de 4 blocs:
- Produit des images et du son
- Transport des signaux résultant (bloc transport)
- Diffusion haute fréquence des images et du son
- La réception par le téléviseur des images et du son associé
Compression en télévision suppose:
- Que les signaux sont numériques
- Que les signaux restent analogiques mais sont déjà échantillonnés.
Télévision numérique suppose que tous les 4 blocs précédemment cités utilisent les signaux numériques. Exemple: TNT (Télévision Numérique Terrestre).
