Expression mathématique

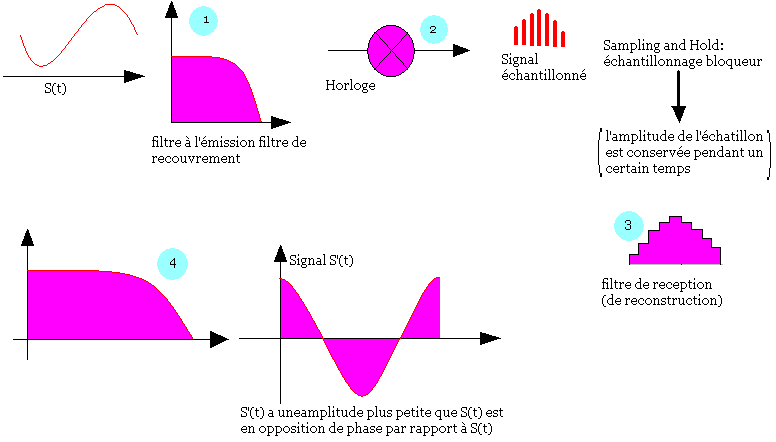
Le signal échantillonné peut être considéré comme étant le produit du signal primaire par une fonction périodique E(t) de période T_e. S_e(t)=S(t).E(t)
L'échantillonnage est équivalente à une modulation d'amplitude du signal S(t) par un train d'impulsion d'amplitude et période constante d'où le nom de Post Amplitude Modulation (PAM)

S(t) est un signal analogique (signal primaire non modulé)
E(t) train d'impulsion d'amplitude et de période constante.
C'est un signal discret disposant des énergies localisées à des instants précis. On peut le considérer comme le signal rectangulaire. S_e)t)=S(t)E(t) : signal modulé en Amplitude disposant des énergies localisée.
La porteuse est un train d'impulsion.

Critère de NIKIST:

F_e: fréquence d’échantillonnage
B: bande passante du signal S(t)
F_e=2B: La fréquence la plus élevé de la bande de fréquence du signal S(t)

Système de transmission PAM

Le signal PAM est un signal échantillonné alors que le MIC est un signal numérique.

Modulation MIC

La modulation MIC (Modulation par Impulsion de Code) est une extension de la modulation PAM. Les échantillons analogiques PAM sont d'abord quantifiés en valeur discrètes puis elles son présentées en nombre entier selon un code.

Bruit de quantification

Le fait de remplacer les échantillons PAM qui peuvent prendre n'importe quelle valeur dans chaque intervalle par les valeurs discrètes d'échantillon dans cet intervalle est à l'origine d'erreur. Cette erreur est due au bruit de quantification. On mesure se bruit par le rapport signal sur bruit (S/B)_q
(S/B)_q = (Puissance du signal)/(Puissance du bruit)
(S/B)_q = E[S(t)²]/E[Y(t)-S(t)]²
E : Moyenne temporelle (Valeur moyenne)
S(t) → Signal analogique à l'entrée
Y(t) → Signal décodé à la sortie.

Loi de quantification uniforme

La quantification peut être linéaire ou non linéaire dans le cas de la quantification linéaire, tous les intervalles de quantification ont la même longueur.

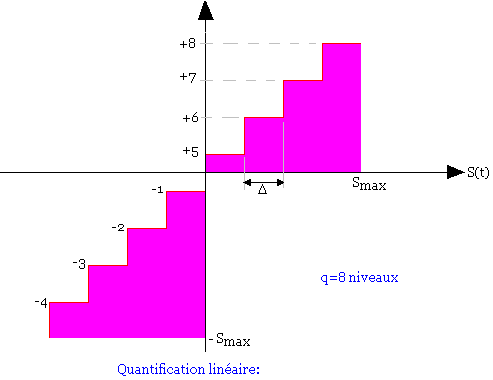
Le rapport signal sur bruit dans ce cas est:

Exemple:

Si nous avons un signal sinusoïdal d'amplitude A_m.

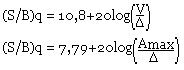
Exercice d'application:
Un signal sinusoïdal d'amplitude 1v doit être quantifié avec un rapport (S/B)_q=30dB.
Combien faut-il d'intervalle de quantification et combien de bit faut-il pour coder chaque échantillon?
Utilisez les polarités positive et négative.

(S/B)_q = 1,76 + 6,02n + 20log₁₀(A/A_max)
A : amplitude du signal sinusoïdale.