Code détecteur et correcteur d’erreur
Le code de Hamming
- Le code de bloc : L'information utile à transmettre se trouve sous forme de bloc de longueur fixe. Il faut ajouter à cette information des bits de contrôle supplémentaires appelé bit de redondance. Seules certaines combinaisons possibles sont acceptées, deux cas se présentent à la réception.
- Le mot reçu est un mot de code, ceci permet au récepteur de reconstituer la véritable information qui a été transmise.
- Le mot reçu ne correspond pas à un mot de code. Dans ce cas le récepteur peut recomposer lui-même le bloc original.
Code détecteur et limiteur d'erreur
Le récepteur pourra aussi demander la retransmission de l'information erronée (code détecteur d'erreur). La distance de Hamming correspond au nombre de bit qui varie entre deux mots successifs de code
Exemple:
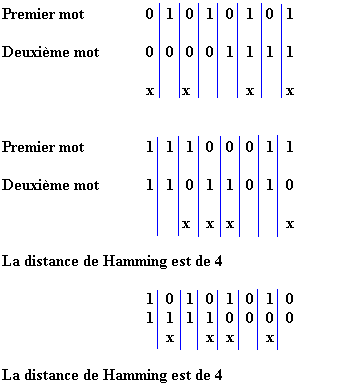
Un code de distance de Hamming = 2 permet la détection d'une seule erreur mais la correction de celle-ci n'est pas réalisable, car on ne connaît pas la position exacte du bit erroné.
|
Distance de Hamming |
Nombre de bits erronés pouvant être détecté |
Nombre de bits erronés pouvant être corrigés |
|
1 |
0 |
0 |
|
2 |
1 |
0 |
|
3 |
2 |
1 |
|
4 |
3 |
1 |
|
5 |
4 |
2 |
Parmi les autres codes de bloque, nous pouvons distinguer:
- VRC (Vertical Redundancy Checking): le code de parité vertical
- LRC (Longitudinal Redundancy Checking)
- Les codes dits "i parmi n": (3B/4B; 4B/5B; 8B/10B ...). Ils permettent la validation des combinaisons comportant i bits de valeur "1" parmi les 2n possibles.
Si nous prenons i=4 et n=8, 70 combinaisons seulement sont valides parmi les 256. Celle-ci comporte chacune 4 bits de valeur "1"
Exemple: Voici deux combinaison issue du code 4 parmi 8
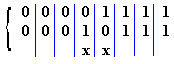
Leur distance de Hamming est de 2
Lorsque le récepteur détecte une erreur, il demande la retransmission du nombre erroné.
NB: Le récepteur contrôle nombre de bit de valeur "1" contenu dans l'information transmise, si ce nombre est différent de 4, il considère que c'est une erreur et redemande la transmission.
Exercice d'application sur le code de contrôle cyclique
10011011 : information à transmettre, nombre de i de bit à transmettre égal 8.
Déterminons le polynôme I(x) correspondant
I(x) = 1 + X + X3 + X4 + X7
Soit G(x) = X3 + 1 qui correspond à 1001
Un polynôme générateur r=4 c'est-à-dire nombre de bit de G(x)
Déterminons le polynôme G(x)-1
G(x) - 1 = 1001 - 1 = 1000
Effectuons le calcul en binaire ci-après
I(x)[G(x)-1]
10011011 x 1000 = 10011011000
Déterminons le polynôme correspondant au produit I(x)[G(x)-1].
Ce polynôme est H(x) = I(x)[G(x)-1]
H(x) = x3 + x4 + x6 + x7 + x10
Trouvons la valeur de H(x) en base 10
(H(x))10 = 1240 ; (G(x))10 = 9
Division 1240 par 9 en division euclidienne.
r=7 = (0111)2
Ajoutons 0111 pour dividendes I(x)
10011011 + 0111 = 10100010
Est-ce que K(x)=I(x)+r est un multiple de G(x)
[K(x)]10 = 162
Ce nombre est divisible par G(x)
Nous avons donc le mot à transmettre sur la ligne ci-après
on réécrit K(x) et on colle le reste "r"
10100010 / 0111
Le mot à transmettre sur la ligne sera 101000100111 = I'
A l'arrivée du message, le récepteur divise I' pas x3+1 si la transmission est bonne, le reste de la division est "0". S'il y'a erreur, le reste est différent de "0".
Pour retrouver la véritable information qui a été envoyée, nous devons effectuer l'opération suivante: on décolle "r" du mot et on soustrait "r" dans ce mot.
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale