Fractions
Une fraction est un rapport a/b dans lequel a et b sont des entiers relatifs et b non nul.
Simplification d'une fraction
Pour simplifier une fraction, on peut procéder de 3 manières:
- On recherche l'ensemble de tous les diviseurs du numérateur et du dénominateur, on simplifie en utilisant le diviseur qui apparaît dans les 2
- Par simplification successive des caractères divisibles
- On recherche le PGCD du numérateur et du dénominateur, on divise par le PGCD des termes de la fraction. Le premier procédé est très long surtout si les nombres sont grands; le deuxième procédé n'aboutit pas toujours à la fraction; le troisième aboutit rapidement, sûrement à la fraction irréductible.
Fractions égales
Deux fractions sont égales si pour obtenir l’une, on doit multiplier ou diviser les termes de l'autre par un même nombre. En simplifiant une fraction, on trouve une fraction qui lui est égale mais avec des termes plus petits.
L'opposé d'une fraction
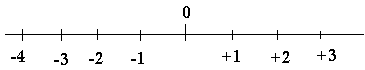
L'opposé d'une fraction est une fraction de signe contraire mais ayant la même distance à zéro.
Exemple: l'opposé de 3/2 est -3/2
L'inverse d'une fraction a/b a pour inverse a/b et a/b x b/a = 1. En multipliant une fraction par son inverse on obtient 1.
Nombres rationnels
Un nombre rationnel est égal à une fraction ou à l'opposé d'une fraction. a/b; a est un entier relatif et b un entier relatif non nul.
Fractions décimales:
Une fraction décimale est telle que le calcul de la division du numérateur par le dénominateur donne un nombre fini.
Fractions algébriques
Lorsque le numérateur et le dénominateur d'une fraction sont des nombres naturels, on dit que cette fraction est une fraction algébrique. L'ensemble des nombres rationnels se note Q
Une fraction dont les termes sont des nombres décimaux peut s'écrire sous la forme d'une fraction algébrique, donc c'est aussi un nombre rationnel.
Opération sur les nombres rationnels
Addition et différence
Il faut d'abord réduire les fractions au même dénominateur.
Méthode:
- On les rend irréductibles en divisant chaque numérateur par leur PGCD
- Trouver le PPCM des dénominateurs de chacune des fractions
- Trouver les fractions respectivement égales à chaque fraction ayant le PPCM comme dénominateur
- Faire la somme des numérateurs et conserver leur dénominateur commun
La multiplication
On multiplie des numérateurs entre eux et les dénominateurs entre eux.
La division
Pour diviser 2 fractions a/b par c/d avec c différent de zéro, on multiplie a/b par l'inverse de c/d donc:
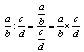
Puissance entière d'un nombre relatif
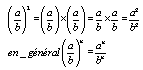
Approximation décimale d'un nombre rationnel
2/3 = 0,666666
Donner une approximation d'ordre d'un nombre c'est donner son écriture jusqu'à un chiffre après la virgule. Exemple: 0,666 est une approximation d'ordre 3 de 8/3, 0 est une approximation à l'unité de 2/3
On distingue une approximation par défaut et une approximation par excès d'un même nombre.
Exemple: 0,66 est l'approximation par défaut d'ordre 2 de 2/3
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale