Fractions algébriques
Lorsque le numérateur et le dénominateur d'une fraction sont des nombres naturels, on dit que cette fraction est une fraction algébrique. L'ensemble des nombres rationnels se note Q
Une fraction dont les termes sont des nombres décimaux peut s'écrire sous la forme d'une fraction algébrique, donc c'est aussi un nombre rationnel.
Opération sur les nombres rationnels
Addition et différence
Il faut d'abord réduire les fractions au même dénominateur.
Méthode:
- On les rend irréductibles en divisant chaque numérateur par leur PGCD
- Trouver le PPCM des dénominateurs de chacune des fractions
- Trouver les fractions respectivement égales à chaque fraction ayant le PPCM comme dénominateur
- Faire la somme des numérateurs et conserver leur dénominateur commun
La multiplication
On multiplie des numérateurs entre eux et les dénominateurs entre eux.
La division
Pour diviser 2 fractions a/b par c/d avec c différent de zéro, on multiplie a/b par l'inverse de c/d donc:
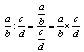
Puissance entière d'un nombre relatif
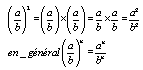
Approximation décimale d'un nombre rationnel
2/3 = 0,666666
Donner une approximation d'ordre d'un nombre c'est donner son écriture jusqu'à un chiffre après la virgule. Exemple: 0,666 est une approximation d'ordre 3 de 8/3, 0 est une approximation à l'unité de 2/3
On distingue une approximation par défaut et une approximation par excès d'un même nombre.
Exemple: 0,66 est l'approximation par défaut d'ordre 2 de 2/3
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale