Pyramides et cônes

Une pyramide est un solide dont la base est un polygone et les faces latérales des triangles.

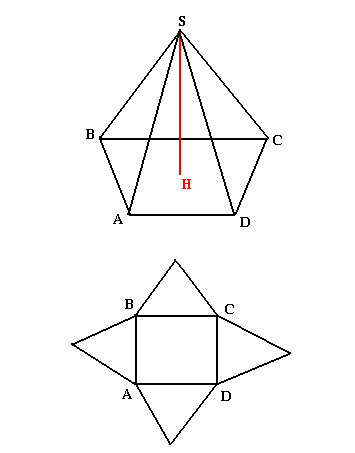
Une pyramide est dite régulière lorsque:

ABCD est la base de la pyramide, SH est la hauteur.
Comme la base est un carré, la pyramide a 4 faces latérales qui sont 4 triangles isocèles superposables.

Volume d'une pyramide

Lorsqu'une pyramide est régulière sont volume est égale à V=1/3.B.h, avec:

Exemple 1

La hauteur d'une pyramide régulière à base carrée est 8Cm, le périmètre de sa base est 16Cm.
Calculons
16 : 4 = 4Cm
V = 1/3.B.h = 1/3 x 4Cm x 4Cm x 8Cm = 128/3 Cm³.

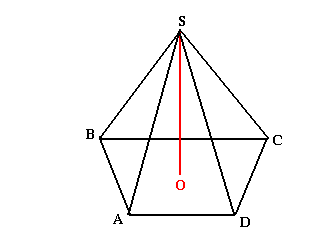
Exemple 2

SABCD est une pyramide régulière à base carrée et sommet S.
1) Faire un dessin.
2) On sait que (AB)=1Cm et que la hauteur mesure 2Cm. Calculez le volume de cette pyramide.
V = 1/3.B.h = 1x1x2/3 = 2/3

Surface latérale, surface totale

La surface latérale d'une pyramide est la surface d'un des 4 triangles qui constitue les surfaces d'une pyramide. Or comme les faces sont les triangles isocèles la surface latérale est égale à base x hauteur/2. La surface totale est égale à la somme de toutes les surfaces latérales.

Exemple

SABCD est une pyramide régulière à base carrée, de sommet S tel que SA=5; AB=4.

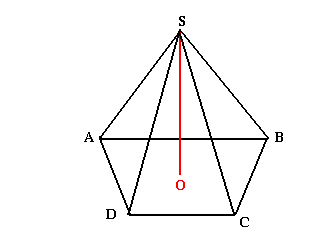
1) Calculez l'aire latérale puis l'aire totale de cette pyramide.

Solution:

S_l= (base x hauteur)/2
S_l = AB.SA/2 = 4x5/2 = 10Cm²