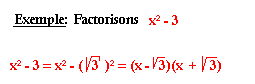Les racines carrées

Soit un entier a on appelle racine carrée de a un entier x tel que x²=a.

Propriété

La racine carrée d'un nombre négatif n'existe pas. Par conséquent pour que la racine carrée d'un nombre existe, il faut que ce nombre soit positif ou nul.

Exemple:

Pour quelle valeur de x, x+2 existe

x+2 exite si et seulement si x+2≥0 ↔ x ≥ -2

Propriété 2

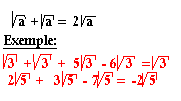
On ne peut additionner les termes semblables.

Propriété 3

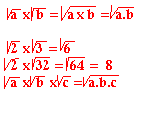
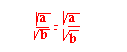
Carrés parfaits

Un carré parfait est un nombre dont on peut extraire la racine carrée à l'aide de la table de multiplication.
Exemple: 0; 1; 4; 16; 25; 36; 49.
Lorsqu'un nombre n'est pas un carré parfait, on peut le décomposer en produit de facteur premier.

Expression conjuguée

On ne doit pas avoir une expression sous radical au dénominateur d'une fraction. Si telle est le cas on rend rationnelle cette expression.
Pour rendre une expression rationnelle, on multiplie le numérateur par le dénominateur par l'expression conjuguée du dénominateur et le dénominateur par sont expression conjuguée simplifiée s'a lieu.

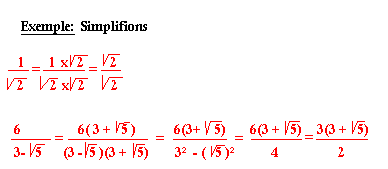
Factorisation

Lorsqu'un nombre n'est pas un carré parfait, on peut faire de lui soit produit de facteur premier soit la racine carrée d'un entier et on obtiendra une identité remarquable de la forme a²-b².