Valeur absolue

La valeur absolue d'un nombre réel est la distance de ce nombre à zéro.
Comme la distance n'est jamais négative, la valeur absolue d'un nombre est toujours positive.
Exemple: |-4|=+4. |+4|=+4; |0|=0; |-9/7|=+9/7

La distance de deux nombres

Soient deux réels A et B, on appelle distance de A à B la différence de leur valeur absolue.
Exemple: Calculez la distance de 2,7 à -1,5
dist(2,7 à -1,5) = |2,7-(-1,5)| = |2,7+1,5| = 4,2

Intervalles

L'ensemble R est l'ensemble des nombres réels.
Il varie de moins l'infini à plus l'infini et comprend 2 sous ensembles R^- et R⁺.

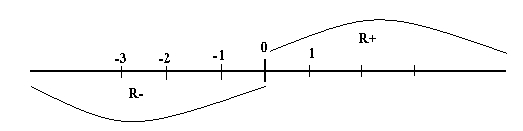
On appelle intervalle dans R une portion de la droite réelle limitée par 2 nombres a et b quelconque. a est la borne supérieure et b la borne inférieure: [a, b]

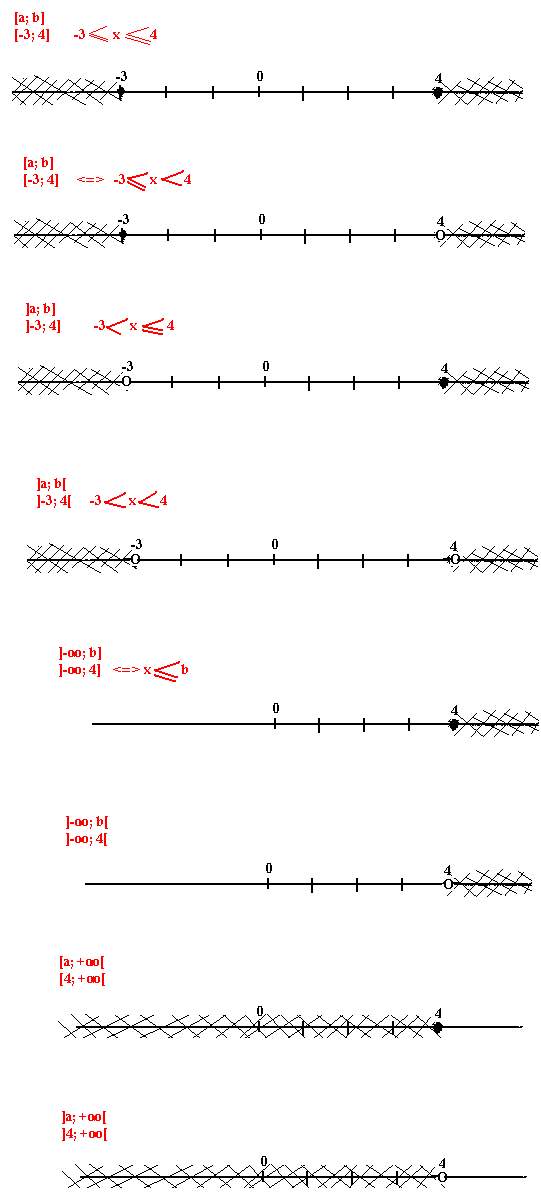
Intersection et réunion de deux intervalles

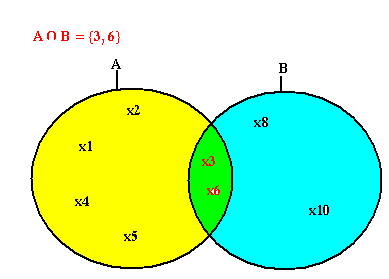
Soient deux ensembles A et B, on appelle intersection de A et B l'ensemble des éléments qu'on retrouve à la fois dans A et dans B
Exemple:
A = {1; 2; 3; 4; 5; 6}
B = {3; 6; 8; 10}
A inter B = {3; 6}

Exemple:

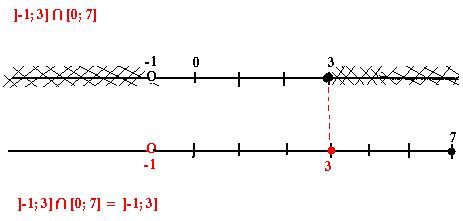
Comparaison des nombres réels

Comparer 2 réels a et b quelconque, c'est montrer leur égalité ou leur inégalité
Exemple:
a=1; b=1; c=-3 alors
a=1; b=1 implique que a=b
1>-3 ↔ a>c
b>c
c<a

Lorsque a est supérieure à b alors a=b est supérieure à 0 et a-b<0. Ainsi

La valeur absolue d'un nombre x est la distance de 0 à ce nombre x. Comme la distance n'est jamais négative, alors la absolue d'un nombre n'est jamais négative. Cependant cette valeur absolue dépend de la position de x dans l'ensemble R.