On appelle équation, une égalité de deux expressions algébriques. Il en existe plusieurs et de degré différents:
- 3x+2=4x-7 (premier degré)
- -x3+7xe=8x-5 (3edégré)
- 2x5-x=3x+2 (5edégré)
- 7x2-2x=3x+6 (2edégré)
Le degré d'une équation correspond au nombre de racine de cette équation.
Equation du 1erdégré
On appelle équation du 1er une équation de la forme ax+b=cx+d oú a, b, c, d sont des coefficients réels distincts et x l'inconnu dont il faut déterminer la valeur.
Exemple:
3x+2=-x-5
2(x+½)=4
Résolution
Pour résoudre une équation du 1er degré de variable x, on regroupe tous les termes contenant x à gauche de l'égalité et tous les termes ne contenant pas x à droite de l'égalité tout en sachant qu'un terme change de signe lorsqu'il change de côté.
Exemples:
4x+5=2x+13
↔ 4x-2x=13-5 ↔ 2x=8
↔ x=8/2
2-7x+3(x-1)=2x+1
↔ 2-7x+3x-1=2x+1
↔ -7x+3x-2x=1-2+3
↔ -6x=2
↔ x=-2/6
↔ x=1/3
Inéquation du 1er degré
On appelle inéquation du 1er degré l'inégalité entre 2 expressions algébriques. Elle est de la forme (inégalité au sens strict):
- ax+b>0
- ax+b<0
Ou encore (inégalité au sens large):
- ax+b≥0
- ax+b≤0
Exemple:
3x+2>4x+9
7x-1≤2x+4
Résolution
La résolution d'une inéquation est identique de celle d'une équation. La solution d'une inéquation se présente sous deux formes: sous la formes graphique ou sous la forme d'intervalles.
Exemple:
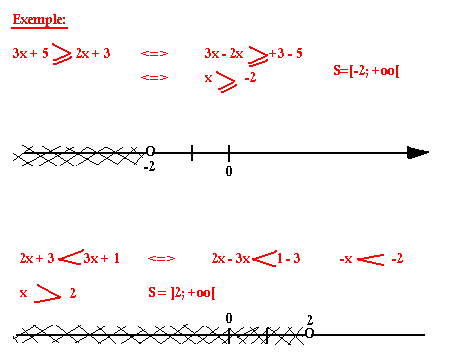
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale