La statistique est l'étude de caractères d'une population donnée. Ce caractère peut être qualitatif ou quantitatif. Exemple: Les élèves du lycée son nombreux et portent le bleu et le gris.
Les statistiques portent essentiellement sur l'organisation des données qui comprennent: les modalités, les effectifs et fréquences. Exemple: Dans une classe de 3e, les notes attribuées aux élèves sont: 1; 10; 11; 0; 3; 2,5; 09; 13.
Gestion des données
On entend par gestion des données toutes les parties du programme correspondant à la proportionnalité et aux statistiques.
Elle s'applique aux sciences, à l'histoire, à la géographie et à la vie courante.
Pourcentage
Exemple 1:
Dans une ville, on a enregistré 25.425 habitants. 16% sont des étrangers, combien d'étranger y'a-t-il dans cette ville?
(25.425x16)/100 = 4.068 habitants
Exemple 2:
On vend un terrain rectangulaire à 1.500€, le m2. Ses dimensions sont telles que la longueur=48m, la largeur=24m. Après une réduction de 12% quel est le montant à payer par l'acheteur?
P = 48x24x1 = 1.728.000x12/100 = 207.306€
1.728.000 - 207.360 = 1.520.640€. P= 1.520.640€
Effectif et fréquence
L'effectif est le nombre d'individu dont il faut étudier le caractère, alors que la fréquence est égale à:
Fréquence=Modalité/effectif total
Exemple 1:
Dans une classe, on a enregistré les notes suivantes en maths: 6; 11; 3; 14; 11; 14; 11; 14; 14; 13; 11; 17; 6; 11; 17; 11.
1) Quel est l'effectif total de cette classe?
2) Dressez un tableau donnant la répartition des notes dans l'ordre croissant et les effectifs.
3) Calculez les fréquences et les fréquences en pourcentage.
Résolution:
|
Modalité, Notes |
3 |
6 |
11 |
13 |
14 |
17 |
|
Effectif |
1 |
2 |
6 |
1 |
4 |
2 |
|
Fréquence |
1/16 |
2/16 |
6/16 |
1/16 |
4/16 |
2/16 |
|
Fréquence en % |
6,25% |
11,5% |
31,5% |
6,25% |
25% |
12,5% |
Diagramme
Le diagramme est un repère sur lesquelles sont représentées les modalités et les fréquences. Ce diagramme peut être circulaire, en bâton ou en bande.
Exemple: Voici la liste des notes des élèves de 3e: 6; 11; 3; 14; 11; 14; 11; 14; 14; 13; 11; 17; 6; 11; 17; 11. Représentez la répartition de ces notes par un diagramme en bâton.
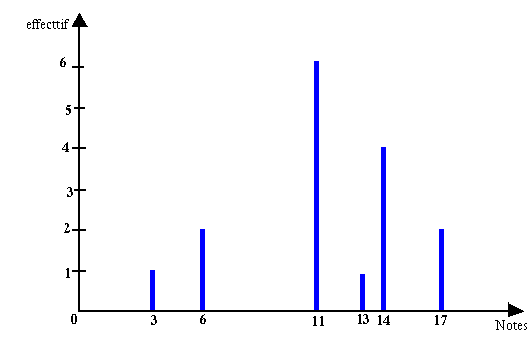
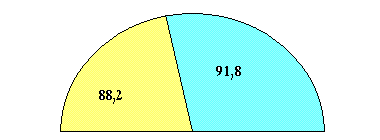
Diagramme circulaire
Pour représenter et calculer les angles correspondants à chaque secteur dans un diagramme semi-circulaire, on divise l'effectif de chaque classe par l'effectif total et on divise le résultat par 180°, puis on multiplie par 360° lorsqu'il s'agit d'un diagramme circulaire.
Exemple:
|
|
Voyelles |
Consones |
Total |
|
Effectif |
25 |
26 |
51 |
|
Fréquence |
25/51 |
26/51 |
1 |
|
Fréquence |
49% |
51% |
100% |
|
Angle ß |
25x180°/51=88,2° |
26x180°/51=91,8° |
180° |
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale