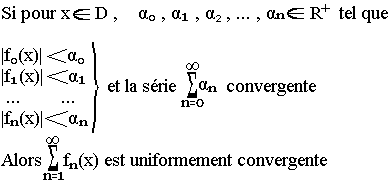Série numérique
Soit (Un)n une suite numérique et (Sn)n la suite des sommes partielles de (Un)n
S1 = U
S2 = U1 + U2
S3 = U1 + U2 + U3
Sp = U1 + U2 + ... + Up
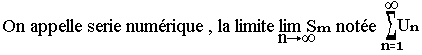
Convergence d'une série
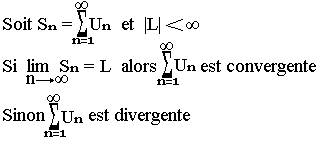
Quelques critères de convergence
Condition nécessaire de convergence
Critère suffisant de convergence
Critère de Alembert
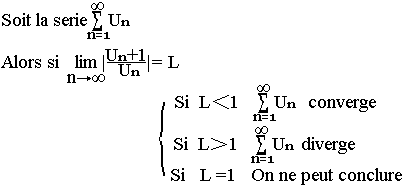
Exemple:
Donnez la nature de la série
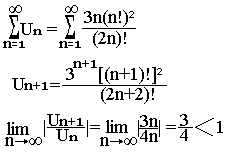
La série converge.
Critère de Cauchy
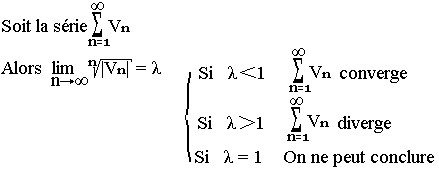
Exemple:
Donnez la nature de la série
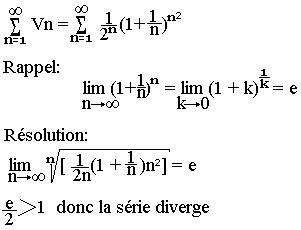
Convergence d'une série (Sn)n de Cauchy
(Sn)n st dite série de Cauchy, elle est convergente.
Critère de convergence de Leibniz
On appelle série alternée, une série de la forme U1-U2+U3+U4-U5-U6+...+(-1)n-1Un+... (E) où les Ui sont tous positifs.
Alors le critère de Leibniz:
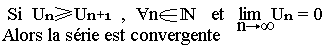
Exemple: Etudiez la convergence de la série:
1/2 - 2/(22+1) + 3/(32+1) - 4/(42+1) + ...
Autres propriétés
Critère de comparaison
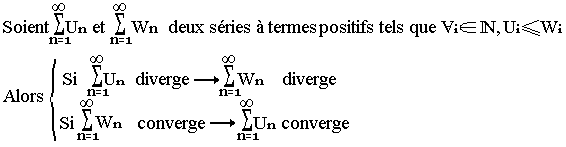
Convergence absolue / Semi convergence
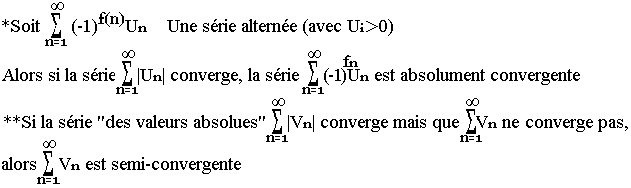
Combinaisons de série
Exercice:
- Déterminez pour quelle(s) valeur(s) de x, la série S(x) est convergente.
S(x) = 1 + e-x + e-2x + e-3x
S(x)=limSk(x) - Calculez la somme de la série 1/1.3 + 1/3.5 + 1/5.7 + 1/5.7 + 1/7.9 + ...
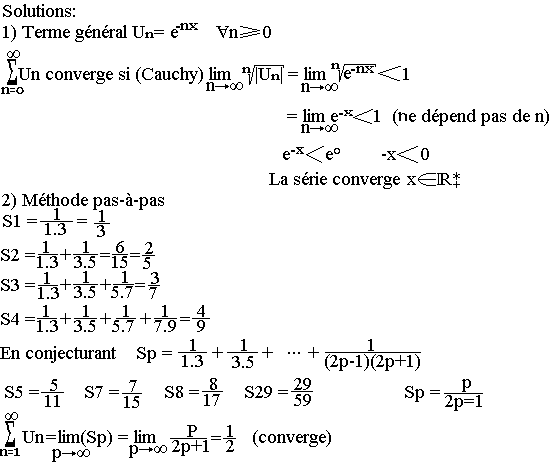
Séries de fonctions
On a appelle série de fonctions, une série de la forme f0(x) +f1(x) +f2(x) +...+fx(x) +.... où les f(x) sont des fonctions continues sur un domaine D.
Domaine de convergence
L'ensemble D des valeurs de x pour lesquelles la série f0(x) +f1(x) +f2(x) +...+fx(x) +.... converge est appelé domaine de convergence de la série.
Convergence uniforme
Dans la suite on considère que
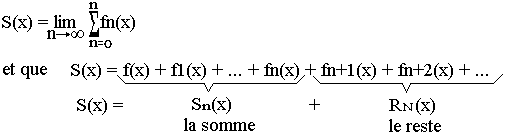
Nous allons définir la notion de convergence uniforme (a) différente de la convergence simple (b) avec b→b
Définition
Une série de fonction simplement convergente est dite uniformément convergente sur un domaine D si
Il existe un autre entier suffisant.
Critère de convergence de Weierstrass
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale