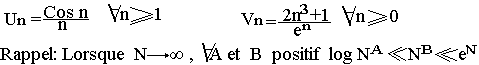Page 1 sur 2
Une suite numérique est une application (Un) définie de N→R par :
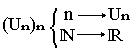
Convergence d'une suite
On dit qu'une suite (Un)b est convergente et converge vers L (L inférieur à l'infini),
La suite est dite divergente si:
Dès que
Opération sur les suites
On va supposer ci-après que deux suites (Un)n et (Vn)n convergentes respectivement vers L et M.
Conséquences
Somme
La suite (Un+Vn)n converge vers L+M.
Produit
La suite (Un.Vn) converge vers LM.
Différence
La suite (Un-Vn) converge vers L-M.
Quotient (avec M différent de 0)
La suite (Un/vn)n converge vers L/M
Proposition
Si une suite admet une limite L (L inférieur à l'infinie) alors celle-ci est unique.
Exemple
Soit la suite (Un)n de terme général Un=(-1)n
- Déterminer les limites respectives des deux sous suites (a2N)n et (b2N+1)n
a2N = U2N
b2N+1 = U2N+1 - Quelle est la limite de la suite (Un)n ?
Sens de variation
Sens de variation
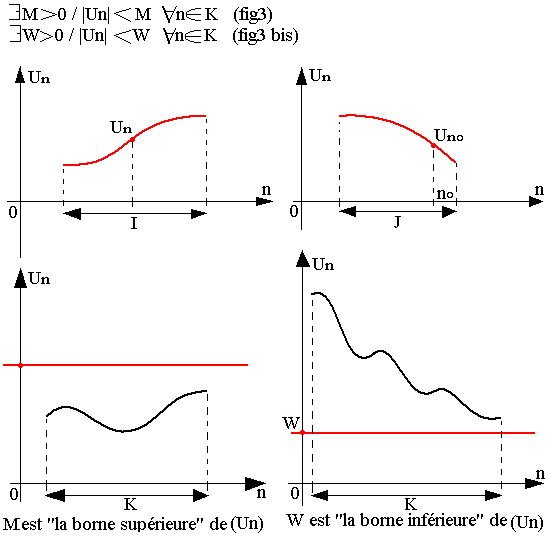
- Une suite Un est croissante sur un intervalle I si Un+1-Un est inférieure ou égale à 0 quelque soit n appartenant à I (fig1) ou encore Un+1/Un est supérieure ou égale à 1 quelque soit n appartenant à I.
- Une suite Vn est décroissante sur un intervalle J si Vn+1-Vn est inférieure ou égale à 0 quelque soit n appartenant à J (fig2) ou encore Vn+1/Vn inférieur ou égale à 1 quelque soit n appartenant à J
Borne d'une suite
On dit qu'une suite (Un)n est basée sur un intervalle K si:
Exercice 1:
Donnez la nature des suites ci-après:
Probatoire A-ABI 2021 Epreuve de littérature ou de culture générale